Passi sulla Luna: Aristoteles
Da Commissione Divulgazione - Unione Astrofili Italiani.
(Creata pagina con '{| width="100%" cellpadding="15" cellspacing="5" |- | bgcolor="silver" | a cura di Alfonso Zaccaria e Paolo Morini <br> {| align="center" border="1" style="font-size: 13px; …')
Differenza successiva →
Versione delle 12:52, 27 ott 2012
|
a cura di Alfonso Zaccaria e Paolo Morini
Il punto rosso sulla faccia della Luna indica la formazione interessata. Per indicare, approssimativamente, in quale periodo del ciclo lunare la formazione è facilmente visibile, la Luna è rappresentata in fase crescente con il terminatore che ha da poco superato la formazione - questo corrisponde a condizioni di illuminazione in luce radente (alba) della formazione stessa.
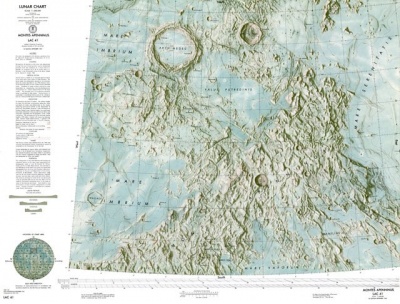
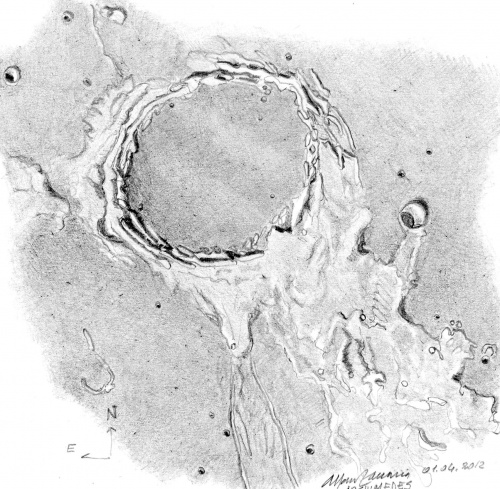
IL NOME Sono giunte a noi pochissime notizie sulla vita di Archimede, uno dei massimi geni dell’antichità. E’ certo che sia nato a Siracusa intorno al 287 a.C. ed ivi morto nel 212, durante la 2a guerra punica. Amico del tiranno Gerone II, visse quasi sempre nella città natale, salvo un breve periodo in Egitto. Inventore, ingegnere, matematico, astronomo, Archimede occupa un posto importantissimo nel campo scientifico del tempo e molte sue realizzazioni ed intuizioni sono tuttora capisaldi della meccanica e della matematica. Sono noti, soprattutto episodi leggendari della sua vita: il grido “Eureka” urlato uscendo nudo dal bagno, felice per aver intuito il principio del peso specifico dei corpi, gli specchi ustori capaci di mandare a fuoco le navi romane di Marcello impegnate nell’assedio di Siracusa e le circostanze della sua morte, quando durante il sacco della città conseguente alla caduta in mani romane, fu ucciso da un legionario per avere rifiutato di seguirlo in quanto impegnato a risolvere un problema matematico. L’attività scientifica di Archimede si esprime in vari campi: nella meccanica, per avere inventato e realizzato ordigni bellici, soprattutto durante l’assedio di Siracusa (catapulte, artigli meccanici oltre ai già citati specchi ustori). La possibilità di calcolare il passare del tempo lo porta a realizzare un orologio ad acqua. Realizza la “vite di Archimede”, un congegno in grado di sollevare materiali sfruttando la rotazione di una spirale. In campo astronomico realizza un planetario meccanico, una parte del quale (simile alla nota macchina di Anticitera) sembra essere stata ritrovata recentemente durante uno scavo a Olbia. Nel campo della geometria si propone nella soluzione della misura del cerchio, giungendo ad una definizione del pi vicinissima alla realtà, utilizzando il metodo dell’esaustione. Questo metodo prevede il calcolo dei perimetri di 2 poligoni, rispettivamente inscritto e circoscritto al cerchio. Archimede usa poligoni di 96 lati e trova che la circonferenza è pari a 3 diametri più una parte minore di 1/7 e maggiore di 10/71 (si ottiene un valore di 3,1419, con un errore di 3/10.000 del valore reale). Studia anche il problema della quadratura della parabola. Studia le spirali, i conoidi, gli sferoidi e i solidi ottenuti tagliando questi con piani obliqui. Studia i corpi galleggianti: le sue formulazioni costituiscono la base dell’idrostatica. Il principio fondamentale porta il suo nome: “un corpo immerso in un fluido riceve una spinta dal basso verso l’alto pari al peso del volume di liquido spostato”. Studia le forme adatte al galleggiamento, sempre orientato alle evidenti applicazioni pratiche, legate alle esigenze del tempo. Nell’”Arenario” affronta il problema della conta dei granelli di sabbia della Terra e, indirettamente, pone l’accento sulla insufficienza della matematica greca nell’affrontare il problema dei grandi numeri. In questo testo e nel “Metodo” si è voluta vedere la precognizione del calcolo infinitesimale, probabilmente un’interpretazione sproporzionata al contesto essenzialmente “pratico” del grande siracusano. Studia e realizza leve e carrucole: famoso l’episodio del varo della grande nave Syracusia che realizza con mezzi meccanici e scarsissimo impiego di energia umana. A questo episodio sembra risalire un’altra famosa frase: “datemi una leva e con essa solleverò il mondo!”. IL CRATERE Situato vicino al bordo orientale del Mare Imbrium, al vertice di un triangolo che ha agli altri vertici Aristillus e Autolycus, è il più grande cratere (85 km) all’interno dello stesso Mare. Ha pareti terrazzate e in parte degradate, alte non più di 1,6 km. Sua caratteristica è la presenza di una specie di promontorio triangolare che si estende dal bordo in direzione S per circa 30 km. Sempre in direzione S si apre l’estesa area montagnosa chiamata Montes Archimedes e dal promontorio sopra descritto originano due rimae (Rimae Archimedes) che attraversano la pianura della Palus Putredinis che separa il cratere dalla grande catena degli Appennini che chiude il Mare a SE. All’interno della Palus, si trova anche Spurr (Archimedes K), quasi totalmente sommerso, che emerge appena con parte delle sue creste più alte. Il fondo di Archimedes, come quello di Plato, è assolutamente piatto, a seguito della fuoriuscita di lava dallo stesso dopo l’impatto. Come si legge in C. A. Wood “The modern Moon”, se Archimedes fosse un cratere simil-Copernico, avrebbe un fondo profondo 4 km ed un picco di 2,4 km di altezza. Invece il picco centrale non c’è, o meglio non si vede in quanto è certamente sommerso dalla lava che ha alzato il fondo fino al livello del piano circostante, come in Plato. Vi sono alcuni craterini vicino ai bordi. Si notano inoltre alcune fasce chiare che attraversano il fondo stesso, verosimile effetto degli ejecta di Autolycus. Vicino ad Archimedes, a SO, c’è un cratere recente (Archimedes A, o Bancroft) di 13 km di diametro e verso N si estende per circa 80 km la catena dei Montes Spitzbergen, chiamati così da Mary Blagg, una astronoma inglese (1858- 1944), per la loro somiglianza con l’omonima isola norvegese, la più grande delle Svalbard. Nei pressi di Archimedes, nel Sinus Lunicus, venne a schiantarsi nel settembre 1959, la navicella sovietica Luna 2, la prima capsula a raggiungere la Luna.
|
||||||||||||||||||||||||||