Il cielo dei navigatori - Introduzione
Da Commissione Divulgazione - Unione Astrofili Italiani.
(→Le proiezioni cartografiche) |
(→Le proiezioni cartografiche) |
||
| Riga 146: | Riga 146: | ||
<br> | <br> | ||
| - | | [[Image: | + | | [[Image:Ilcielodeinavigatori PB2.GIF]] |
|} | |} | ||
{| | {| | ||
|- | |- | ||
| - | | | + | | [[Image:Ilcielodeinavigatori PD.GIF]] |
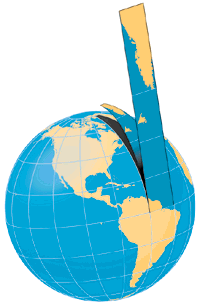
| La proiezione di Mercatore, per esempio, fa aumentare le aree procedendo | | La proiezione di Mercatore, per esempio, fa aumentare le aree procedendo | ||
dall'equatore verso i poli. Nella figura lo spicchio contenente la Groenlandia si proietta in un rettangolo che, all'equatore si confonde con la corrispondente superfice della sfera, ma ai poli aumenta enormemente la superficie proiettata di questa penisola. | dall'equatore verso i poli. Nella figura lo spicchio contenente la Groenlandia si proietta in un rettangolo che, all'equatore si confonde con la corrispondente superfice della sfera, ma ai poli aumenta enormemente la superficie proiettata di questa penisola. | ||
| Riga 163: | Riga 163: | ||
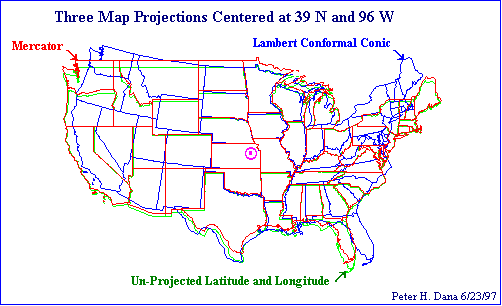
stessa area, vengono così a non essere sovrapponibili e questo tanto pi&ugrave quanto più ci si allontana dal centro di proiezione. Nella figura sono state sovrapposte tre proiezioni degli Stati uniti, aventi lo stesso centro; notate che, lontano da esso, le differenze sono notevoli, tali da dar luogo a tre rappresentazioni ben separate della penisola della Florida. | stessa area, vengono così a non essere sovrapponibili e questo tanto pi&ugrave quanto più ci si allontana dal centro di proiezione. Nella figura sono state sovrapposte tre proiezioni degli Stati uniti, aventi lo stesso centro; notate che, lontano da esso, le differenze sono notevoli, tali da dar luogo a tre rappresentazioni ben separate della penisola della Florida. | ||
| - | | | + | | [[Image:Ilcielodeinavigatori TP.GIF]] |
| <br> | | <br> | ||
|} | |} | ||
| Riga 173: | Riga 173: | ||
{| | {| | ||
|- | |- | ||
| - | | | + | | [[Image:Ilcielodeinavigatori DIS.GIF]] <center>Proiezione azimutale equidistante</center> |
| | | | ||
Il cartografo può voler conservare in scala tutte le distanze che intercorrono tra i luoghi della regione rappresentata, in questo caso la proiezione si chiama '''equidistante''': il rapporto tra due distanze sulla carta è uguale al rapporto tra le corrispondenti distanze nella realtà. <br> Generalemte solo le carte topografiche, con rapporto di scala 1:25.000 od inferiore, sono equidistanti; nelle proiezioni a scala maggiore l'equidistanza si mantiene solo lungo una determinata direzione. Un esempio di proiezione equidistante è la '''proiezione azimutale equidistante''' | Il cartografo può voler conservare in scala tutte le distanze che intercorrono tra i luoghi della regione rappresentata, in questo caso la proiezione si chiama '''equidistante''': il rapporto tra due distanze sulla carta è uguale al rapporto tra le corrispondenti distanze nella realtà. <br> Generalemte solo le carte topografiche, con rapporto di scala 1:25.000 od inferiore, sono equidistanti; nelle proiezioni a scala maggiore l'equidistanza si mantiene solo lungo una determinata direzione. Un esempio di proiezione equidistante è la '''proiezione azimutale equidistante''' | ||
| Riga 184: | Riga 184: | ||
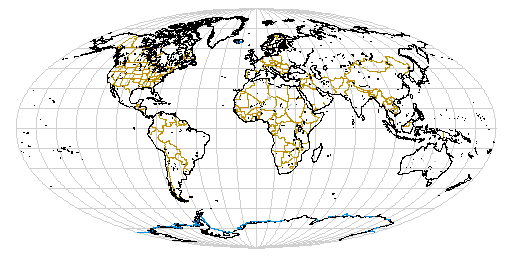
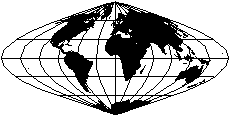
nelle proiezioni '''equivalenti''', si conservano le aree: due superfici sulla carta stanno nello stesso rapporto che intercorre tra le corrispondenti superfici nella realtà. Per le latitudini intermedie la proiezione '''sinusoidale''' realizza l'equivalenza. | nelle proiezioni '''equivalenti''', si conservano le aree: due superfici sulla carta stanno nello stesso rapporto che intercorre tra le corrispondenti superfici nella realtà. Per le latitudini intermedie la proiezione '''sinusoidale''' realizza l'equivalenza. | ||
| - | | | + | | [[Image:Ilcielodeinavigatori AREA.GIF]]> <center>'''Proiezione sinusoidale'''</center> |
|} | |} | ||
| - | {| | + | {| |
|- | |- | ||
| - | | | + | | [[Image:Ilcielodeinavigatori DIRECT.GIF]] <center>Proiezione del Mercatore</center> |
| Nelle proiezioni '''isogone''' o '''conformi''' si conservano gli angoli | | Nelle proiezioni '''isogone''' o '''conformi''' si conservano gli angoli | ||
| - | tra due direzioni qualsiasi e quindi vengono mantenute le forme degli oggetti rappresentati. La | + | tra due direzioni qualsiasi e quindi vengono mantenute le forme degli oggetti rappresentati. La |
| - | + | '''proiezione di Mercatore''' è una proiezione conforme: forme e direzioni sono corrette, ma non certo le aree. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | Si noti che in questa proiezione paralleli e meridiani si incontrano formando angoli retti, come nella realtà. <br> | |
| - | + | ||
| - | + | {| | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
== La geometria delle proiezioni cartografiche == | == La geometria delle proiezioni cartografiche == | ||
Versione delle 09:32, 1 nov 2010
ATTENZIONE ! - PAGINA IN CORSO DI COMPLETAMENTO !!!
SI DECLINA OGNI RESPONSABILITA' IN MERITO ALLE INFORMAZIONI TRATTE DALLA PRESENTE IN QUANTO NON ANCORA CONTROLLATE E RILASCIATE
Incontriamoci
Incontriamoci: è semplice a dirsi, ma può risultare difficile a farsi. Se uno ci dice incontriamoci e basta è molto probabile che non ci si trovi mai. Perché? Ma è chiaro, non abbiamo detto dove e quando. Ma "dove" ha senso solo se conosciamo il luogo dove ci dobbiamo incontrare e se è ben caratterizzato e circoscritto; provate a prendere un appuntamento in una città, anche piccola, che non conoscete, avrete difficoltà a trovarvi. E anche per il "quando" è lo stesso problema, se non sappiamo riconoscere il momento per il quale è fissato l'appuntamento è probabile che si aspetti a lungo e, forse, inutilmente.
In alcuni casi particolari ce la possiamo fare: possiamo incontrarci, per esempio, davanti alla chiesa principale di una città e al tramonto. In questo caso si dovrà domandare a qualcuno dove si trova la chiesa principale e dovremo guardare il Sole, aspettando che tramonti. Se ci incontriamo in una zona disabitata bisognerà descrivere bene il luogo dell'appuntamento e che questo sia ben riconoscibile; nessuna descrizione risulterà di qualche utilità se ci troviamo in mezzo al mare, nella foresta equatoriale od in un deserto sabbioso o roccioso. E se volessimo incontrarci in un momento della giornata diverso dal tramonto, come riconoscerlo? Potremmo convenire di incontrarci nella prima parte del giorno, durante la mattina, quando ancora il Sole sta salendo nel suo cammino diurno, oppure nel pomeriggio, quando il Sole ha iniziato a scendere. In ogni caso non sapremo mai determinare con precisione il momento e la cosa migliore sarebbe di presentarsi con un certo anticipo, ma quanto tempo sprecato!
Incontrarsi non è facile a meno di non avere una carta dei luoghi (carta topografica) e un orologio. Ambedue sono delle invenzioni abbastanza recenti e se venite con noi andremo a scoprire come gli uomini hanno imparato a conoscere la loro posizione, in terra e in mare, guardando le stelle e rendendosi conto che per definire il quando, ma anche il dove, era indispensabile l'orologio.
I nomi dei luoghi
I luoghi hanno un nome: Firenze, Roma, Parigi, Londra, ma anche più semplicemente l'Impruneta, l'EUR, S.Siro ecc. Ogni volta che si pensa al nome di un luogo ci viene in mente dove è, cioè si pensa al suo posto negli altri e tra gli altri luoghi: Roma è in Italia, Londra in Inghilterra, Parigi è in Francia ed è tra Roma e Londra. Insomma i luoghi hanno un posto, ognuno diverso dall'altro.
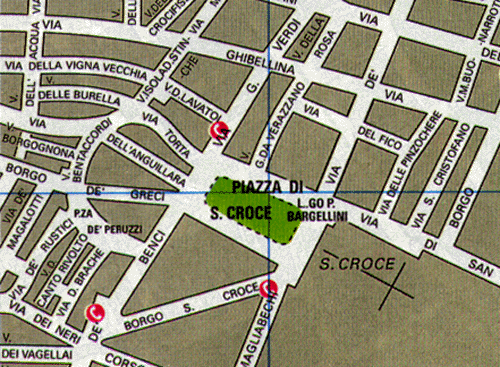
Talvolta il nome rappresenta una vera e propria descrizione delle caratteristiche del luogo cui si riferisce. Ma non sempre è facile riconoscere questa descrizione o servirsene per individuare il luogo, a causa dei cambiamenti linguistici, morfologici ecc. intervenuti nel tempo. Per esempio a Firenze una strada cittadina si chiama "Via Torta" ed in effetti ancora oggi essa corre tutt'intorno ad un isolato, sorto su i resti di un antico anfiteatro romano.
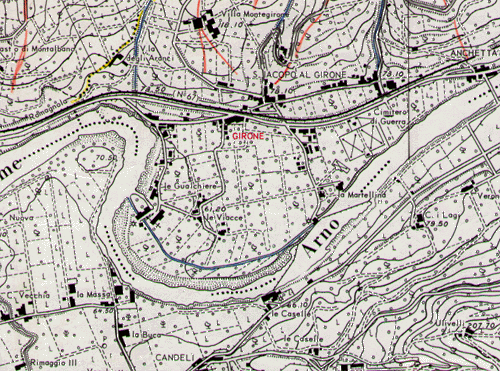
Ad Est di Firenze una piccola frazione si chiama "Il Girone". Qui il corso del fiume Arno è tortuoso perchè, nel terreno pianeggiante, si è formato anticamente un meandro.
Dietro il nome dei luoghi si cela spesso una grande ricchezza culturale: storia, geografia, costume ecc. Ma se dovessimo utilizzare il nome dei luoghi ed il loro significato per riconoscerli, come facevano un tempo contadini, pastori, cacciatori, la nostra mobilità sarebbe molto limitata: impieghremmo dei giorni per spostamenti anche di sole poche decine di chilometri !
I posti dei luoghi
Ogni luogo ha un posto tra gli altri luoghi, ma come fare a comunicare il posto di un luogo? Ecco che nasce spontanea l'esigenza di disegnare su un foglio di carta il posto di un luogo tra gli altri luoghi, per spiegare al nostro interlocutore come fare ad arrivarci. In breve quel foglio di carta diventa la carta o la mappa che indica il posto del luogo. La storia della Geografia è la storia di come l'Uomo ha imparato a fare le mappe per descrivere i posti dei luoghi. Non a caso la parola Geografia, in greco, significa la scienza del disegno della Terra.
È molto importante, nella preparazione di una carta, che si conservino le proporzioni delle distanze tra luogo e luogo. Se non si obbedisce a questa semplice regola, il viaggiatore non potrà pianificare correttamente i tempi di percorrenza del suo viaggio. Siccome però la carta è molto più piccola rispetto alle distanze che intercorrono tra i luoghi che vuole rappresentare, si dovranno ridurre le distanze di un fattore di scala, semplicemente chiamato: scala. Ovvero si dovrà decidere a quale distanza nella realtà, corrisponde un centimetro sulla carta. Se si vuole rappresentare una regione molto grande, molti chilometri corrisponderanno ad un centimetro, se invece si vuole rappresentare una regione piccola, saranno pochi i chilometri che corrispondono ad un centimetro.
Rispetto alla scala le carte si dividono in:
- Planisferi: un centimetro corriponde a 1000 chilometri o più
- Carte Generali: un centimetro corrisponde a distanze comprese tra 1000 e 10 chilometri
- Carte Corografiche: un centimetro corrisponde a distanze comprese tra 10 e 1,5 chilometri
Via via che diminuisce il rapporto di scala, nelle carte si può rappresentare un numero sempre più grande di particolari: abitati, fiumi, torrenti, laghi, strade e ferrovie e, addirittura, il tipo di vegetazione dei boschi e dei campi rappresentati nelle carte topografiche.
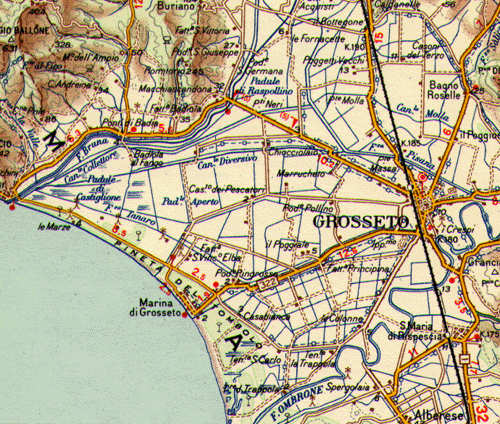
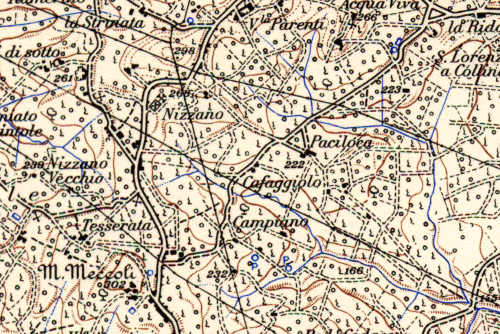
- Nelle carte Topografiche un centimetro va da 1,5 chilometri a 100 metri. In Italia sono molto diffuse le "tavolette" dell'Istituto Geografico Militare (I.G.M.) la cui scala è 1:25.000, un centimetro corrisponde a 250 metri.
Un centimetro corrisponde a 100 metri. La carta è centrata nella località "Cafaggiolo".
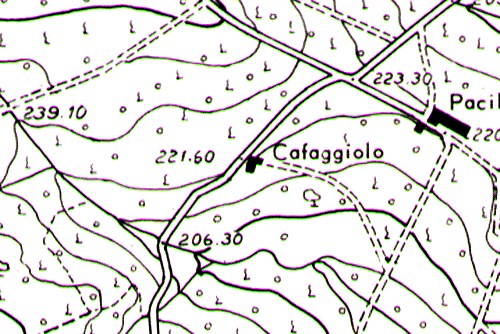
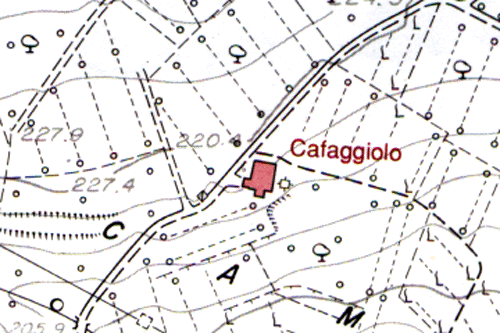
- Nelle Piante o Mappe un centimetro corrisponde a meno di 100 metri.
Un centimetro corrisponde a 50 metri. La carta è centrata nella località "Cafaggiolo".
I posti sulla Terra sono individuati dalle loro coordinate geografiche: una rete di riferimento che consente di determinare il posto di ogni luogo, mediante la sua latitudine e la sua longitudine.
La Terra è una sfera anche se non sembra
La Terra è un Pianeta e, come gli altri pianeti, è un corpo di forma sferica, isolato nello spazio. Queste affermazioni non scaturiscono direttamente dall'esperienza quotidiana, in quanto normalmente viviamo sulla superficie del pianeta che, per le sue dimensioni, ci appare piatta. Oggi, però, abbiamo a disposizione immagini dallo spazio che fanno ormai parte della vita di tutti i giorni: documentari televisivi, servizi meteorologici; queste immagini, meglio di qualunque argomentazione, dimostrano che la Terra è un pianeta.
L'uomo ha intuito e dimostrato la sfericità della Terra anche prima dell'era spaziale, basandosi su diverse esperienze, alcune delle quali, le più semplici, sono qui elencate, proprio perchè chiunque possa ripeterle, senza nessuna particolare attrezzatura ed apprezzando fino in fondo il lungo cammino della Scienza.
1. Se dalla riva del mare vediamo avvicinarsi una nave, ci accorgiamo che per primi compaiono gli alberi, le ciminiere e le parti più alte del ponte e poi, ultimo, lo scafo. Il contrario si verifica se la nave si allontana. Tutto questo non avverrebbe se la Terra fosse piatta.
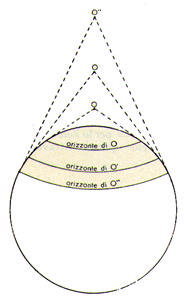
2. Per un osservatore che si arrampica lungo i fianchi di una montagna l'orizzonte, pur rimanendo circolare, s'ingrandisce via via che aumenta la quota. Tra le infinite figure geometriche solo la sfera ha la proprietà di apparire circolare, da qualsiasi punto la si osservi. 3. Nello stesso istante il cielo diurno o notturno appare diverso ad osservatori posti in luoghi diversi della Terra. In particolare, se ci muoviamo verso Sud, le stelle meridionali ci appaiono via via più alte e sempre più basse quelle settentrionali. Viceversa se ci muoviamo verso Nord. Se due osservatori, in luoghi a diversa longitudine, osservano contemporaneamente il cielo, quello che si trova ad Est vede le stesse stelle in posizione più occidentale dell'altro e viceversa per l'osservatore che si trova più ad Ovest.
4. Durante le eclissi di Luna l'ombra della Terra, proiettata sul nostro satellite, è circolare. Solo un corpo sferico, comunque illuminato, può proiettare un'ombra sempre circolare.
5. Anche usando un piccolo telescopio gli altri corpi del sistema solare ci appaiono di forma sferica ed isolati nello spazio. Per analogia questo dovrebbe valere anche per la Terra.
Le dimensioni della Terra
La Terra non è esattamente sferica, infatti:
- Il diametro equatoriale è leggermente superiore a quello polare.
- La sua superficie presenta valli e montagne, punti più alti e punti più bassi rispetto a qualsiasi livello medio.
Possiamo quindi definire la Terra un ellissoide di rotazione (una specie di pallone da rugby) rugoso. Non dimentichiamo però che schiacciamento e rugosità sono del tutto trascurabili rispetto alle sue dimensioni, ed è per questo che, dallo spazio, ci appare perfettamente sferica. Lo possiamo constatare dalle seguenti misure:
| Raggio Equatoriale (R) | Km. 6.378,4 |
| Raggio Polare (R') | Km. 6.356,9 |
| Differenza (R - R') | Km. 21.5 |
| Schiacciamento ([R - R']/R) | |
| Circonferenza equatoriale | Km. 40.076,6 |
| Lunghezza del Meridiano | Km. 40.008,9 |
| Superficie | Km2. 509.950,414 |
| Volume | Km3. 1.083.000.000 |
| Monte Everest | m. 8.882 |
| Fossa di Emden | m. -10.793 |
(L'immagine dell'eclissi di Luna ci è stata data dall' Osservatorio Torre Luciana.)
Le proiezioni cartografiche
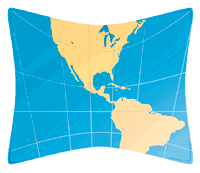
Il problema che deve affrontare chi disegna le carte geografiche consiste nel trovare un accorgimento per rappresentare una superficie sferica (la Terra) su un foglio piano (la carta geografica). Il problema non si pone quando si vogliono rappresentare piccolissime porzioni di superficie terrestre (per esempio le carte catastali), ma diventa notevole quando le aree da rappresentare sono molto grandi. Si parla allora di proiezioni cartografiche, cioè di un insieme di regole che permettono di riportare sul piano della carta ogni punto della superficie terrestre rappresentata. Non è possibile spianare una superficie sferica o, più in generale curva, senza deformarla, cioè senza apportare compressioni ed espansioni ad alcune, se non a tutte le sue parti.
| Non è possibile spianare una superficie sferica o, più in generale curva, senza deformarla, cioè senza apportare compressioni ed espansioni ad alcune, se non a tutte le sue parti.
| 
|
Si può però scegliere quali distorsioni introdurre e quali proprietà conservare.
<A NAME="equidistante">
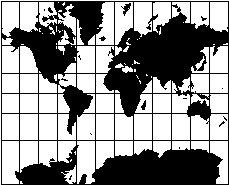 | Nelle proiezioni isogone o conformi si conservano gli angoli
tra due direzioni qualsiasi e quindi vengono mantenute le forme degli oggetti rappresentati. La proiezione di Mercatore è una proiezione conforme: forme e direzioni sono corrette, ma non certo le aree. Si noti che in questa proiezione paralleli e meridiani si incontrano formando angoli retti, come nella realtà. |