Da Commissione Divulgazione - Unione Astrofili Italiani.

Versione delle 09:23, 1 nov 2010 (visualizza sorgente) Paolomorini (Discussione | contributi) (Creata pagina con 'gg') ← Differenza precedente		Versione delle 09:35, 1 nov 2010 (visualizza sorgente) Paolomorini (Discussione | contributi) Differenza successiva →
Riga 1:		Riga 1:
-	gg	+	=Ottobre=
		+
		+	[[Image:Ilcielodeinavigatori OCTOBER.GIF|center]]
		+
		+
		+	Ottobre: si ara e si semina nei campi.
		+
		+	['''Per tornare alla pagina precedente usare il bottone back del browser''']
		+
		+
		+	=Ogigia=
		+
		+	È l'isola del Mediterraneo occidentale in cui, secondo Omero, viveva Calipso. Molto probabilmente si tratta di un luogo immaginario in quanto ogni tentativo di identificazione è risultato inconsistente.
		+
		+	['''Per tornare alla pagina precedente usare il bottone back del browser''']
		+
		+	=Paralleli=
		+
		+	[[Image:Ilcielodeinavigatori PARALLEL.GIF|center]]
		+
		+
		+	La Terra ha una forma molto vicina alla sfera. In una sfera non ci sono punti particolari come sono i vertici per esempio di un cubo, ma se la sfera si mette a ruotare ecco che due punti della sfera assumono una grande importanza sono i poli dell'asse di rotazione. Sono cioè quei due punti, diametralmente opposti, in cui l'asse di rotazione incontra la superficie della sfera.
		+	Se consideriamo i piani perpendicolari all'asse di rotazione che intersecano la sfera, vediamo che ognuno di essi taglia la sfera lungo cerchi il cui diametro è tanto più piccolo quanto più il piano è vicino ad un polo della sfera Questi cerchi vengono detti circoli paralleli o paralleli.
		+	Il cerchio più grande è detto cerchio equatoriale ed è quello che si ottiene tagliando la sfera con un piano equidistante dai due poli e quindi passante per il suo centro. I paralleli sono tutti Piccoli circoli con esclusione dell'Equatore che è un Grande circolo
		+
		+	['''Per tornare alla pagina precedente usare il bottone back del browser''']
		+
		+
		+	=Pitea, esploratore avventuroso (e fantasioso) del IV secolo a.C.=
		+
		+	Pitea, navigatore greco originario della colonia di Massalia (la moderna Marsiglia), fu il primo greco a descrivere la costa nord-occidentale dell'Europa, compresa la Gran Bretagna. Il suo libro principale sull'"Oceano" è stato perduto, tuttavia le sue descrizioni sono state ampiamente copiate dai geografi che sono vissuti dopo di lui, in particolare Eratostene e Posidonio, altri invece come Polibio e Strabone considerarono le sue descrizioni come pure fantasie. Tuttavia, è sicuro che Pitea abbia veramente percorso le coste europee spingendosi molto a Nord; questa certezza deriva dalle descrizioni delle usanze dei popoli incontrati, ma soprattutto dalle indicazioni che Pitea dà sulla lunghezza dell'ombra dello gnomone al solstizio d'Estate a quelle latitudini. Tra le descrizioni di questo avventuroso navigatore greco troviamo anche quelle della lontana Tule, una città che si sarebbe dovuta trovare a sei giorni di navigazione delle coste settentrionali dell'Inghilterra, ed il cui territorio si estendeva verso il circolo polare artico.
		+
		+	['''Per tornare alla pagina precedente usare il bottone back del browser''']
		+
		+
		+	=Pleiadi=
		+
		+	[[Image:Ilcielodeinavigatori M45.GIF|center]]
		+
		+
		+	L'ammasso delle Pleiadi osservato con un binocolo astronomico
		+	Le Pleiadi costituiscono l'ammasso di stelle forse più famoso. Si trovano nella costellazione del Toro a Nord Ovest della stella più luminosa, Aldebran. Ad occhio nudo se ne vedono sette, difatti le Pleiadi sono note anche come le "sette sorelle". Con un buon binocolo, e con il cielo sufficientemente scuro, si scopre che l'ammasso, il cui diametro è all'incirca uguale a quello della Luna, è costituito da centinaia di stelle a cui è associata una debole nebulosità.
		+
		+	[[Image:Ilcielodeinavigatori TAURUS.GIF|center]]
		+
		+
		+	La costellazione del Toro da Johann Hevelius:
		+	URANOGRAPHIA (1690) (la freccia indica l'ammasso delle Pleiadi).
		+	L'immagine appartiene alla collezione storica del Museo astronomico di Brera, disponibile in rete . Nella cartografia celeste dell'epoca i punti cardinali Est ed Ovest risultano invertiti in quanto il cielo viene rappresentato come un globo celeste visto dall'esterno.
		+	Queste stelle hanno eccitato la curiosità fino dall'antichità e qualche volta sono state considerate esse stesse una costellazione. Per i Greci esse erano le figlie di Atlante e Pleione, che sono l'ottava e la nona stella del gruppo in ordine di luminosità decrescente. Secondo un'altra leggenda esse erano le compagne di caccia della dea Artemide, che, quando vennero molestate dal brutale cacciatore Orione, furono strappate alla terra dalla loro protettrice e poste in cielo. Spesso nelle leggenda vengono anche indicate come le stelle piangenti. Potrebbero piangere per la scomparsa di una sorella, la stella Sterope, che nel tempo si è molto indebolita e quindi si perde facilmente nell'osservazione ad occhio nudo.
		+
		+	['''Per tornare alla pagina precedente usare il bottone back del browser''']
		+
		+
		+	=La Precessione degli Equinozi=
		+
		+	[[Image:Ilcielodeinavigatori PRECESS2.GIF|center]]
		+
		+
		+	L'attrazione gravitazionale della Luna e del Sole tende a modificare la direzione dell'asse di rotazione terrestre facendole descrivere, in senso orario, la superficie di un cono in poco più di 26.000 anni. L'asse di questo cono è perpendicolare al piano dell'orbita terreste ossia dell'eclittica. Di conseguenza i poli celesti descrivono un cerchio attorno ai corrispondenti poli dell'eclittica, mantenendosi a 23° e 26' da essi. Il piano equatoriale è solidale con l'asse di rotazione, per cui i suoi punti d'intersezione con l'eclittica (chiamati il punto Gamma ed il punto Omega) scorrono lentamente in senso orario, muovendosi di circa 50" all'anno.
		+	Gli equinozi (il punto Gamma ed Omega) sembrano precedere le stelle verso il tramonto, da qui il nome di Precessione degli Equinozi che viene dato a questo fenomeno. Il punto Gamma, muovendosi apparentemente in senso orario lungo l'eclittica, va incontro al Sole che si muove, in senso antiorario, sullo stesso piano. Per questo motivo, l'anno tropico è di circa 20 minuti più breve dell'anno sidereo. L'anno tropico dura 365.2422 giorni, ovvero 365g 5h 49m, mentre l'anno sidereo 365.253 ovvero 365g 6h 9m.
		+	Il fenomeno della Precessione, modificando la posizione dell'Equinozio di Primavera rispetto alle stelle, comporta il cambiamento sia dell'ascensione retta che della declinazione.
		+	La Precessione degli Equinozi non ha praticamente alcun effetto sul pianeta Terra, in quanto lascia invariata l'inclinazione dell'eclittica, da cui dipende l'ampiezza della variazione stagionale dell'inclinazione dei raggi solari, che scaldano il suolo terrestre. La manifestazione più evidente della Precessione è lo spostamento del Polo Nord Celeste tra le stelle e quindi l'avvicendamento, nel tempo, delle stelle polari, cioè delle stelle luminose che, di volta in volta, risultano più vicine ad esso. Nelle cartine seguenti la lettera P indica il polo nord celeste.
		+
		+	[[Image:Ilcielodeinavigatori NORD_NOW.GIF|center]]
		+
		+
		+	Il cielo a Firenze a meta' di Aprile del 1998
		+	La Polare attuale è la stella alfa Ursae Minoris (UMI), ma 2500 anni fa era Kosciab, la beta della stessa costellazione.
		+
		+	[[Image:Ilcielodeinavigatori NORD_AC.GIF|center]]
		+
		+
		+	Il cielo a Firenze a metà di Aprile di 2500 anni fa
		+	e sarà la stella Vega, l'alfa della Lira (LYR) tra 11.000 anni
		+
		+	[[Image:Ilcielodeinavigatori NORD_DC.GIF|center]]
		+
		+
		+	Il cielo a Firenze a metà di Aprile tra 11.000 anni
		+	Dalla variazione delle coordinate equatoriali delle stelle al passare del tempo, deriva anche che le stelle circumpolari (quelle che non sorgono nè tramontano in un dato luogo) possono diventare occidue (quelle che sorgono e tramontano) e le stelle occidue diventare invisibili (quelle che non sorgono mai) e viceversa.
		+
		+	Altre informazioni sulla precessione in rete nei seguenti siti:
		+
		+	Dimostrazione della Precessione nel laboratorio di Fisica
		+	Precession of the Equinoxes Una spiegazione completa, ma con tanta matematica
		+	Il mito di Mitra spiegato con la precessione.
		+
		+	['''Per tornare alla pagina precedente usare il bottone back del browser''']
		+
		+
		+	=Le proiezioni prospettiche=
		+
		+	Le proiezioni prospettiche si distinguono in proiezioni polari, equatoriali o qualsiasi, a seconda che il polo di proiezione (punto di tangenza della sfera con il piano di proiezione) sia uno dei poli terrestri o si trovi sull'equatore o coincida con un punto qualsiasi della superficie terrestre. In ciascuno dei casi la proiezione potrà essere centrografica, stereografica, od ortografica, a seconda della posizione del punto vista. Nella proiezione centrografica, il punto di vista è al centro della sfera, in quella stereografica è nel punto diametralmente opposto al polo di proiezione, mentre in quella ortografica si trova all'infinito.
		+
		+	Nella pratica cartografica si rivelano molto più utili le proiezioni azimutali modificate, in modo da conservare, con opportuni algoritmi, alcune o tutte le proprietà cartografiche. Alcuni esempi:
		+
		+	[[Image:Ilcielodeinavigatori AZME.GIF|center]]
		+
		+
		+	La proiezione azimutale equidistante raffigurata è una proiezione polare, centrografica modificata. I meridiani sono rettilinei, i paralleli concentrici e volutamente ed arbitrariamente equidistanziati. In questo modo l'equidistanza è assicurata lungo ogni direzione a partire dal centro che, in questo caso, coincide con il polo geografico, essendo l'asse terrestre perpendicolare al piano di proiezione. Le lossodromiche che si irradiano dal centro coincidono con i meridiani e sono quindi rettilinee.
		+
		+	[[Image:Ilcielodeinavigatori LAMA.GIF|center]]
		+
		+
		+	Anche in questo caso la proiezione e' polare, centrografica e modificata. La modifica consiste nel garantire l'equivalenza delle superfici. In questa proiezione i paralleli non sono equidistanziati e tendono ad avvicinarsi verso la periferia della carta.
		+
		+	[[Image:Ilcielodeinavigatori NSTERE.GIF|center]]
		+
		+
		+	La proiezione stereografica è una proiezione puramente geometrica, non modificata. Quella raffigurata è polare con il punto di vista nel Polo Sud geografico. Nella proiezione stereografica gli angoli compresi tra due circoli sulla sfera vengono conservati sulla carta. quindi la proiezione è isogonica e conforme: i continenti mantengono la loro forma. Questo non è però vero per le aree, che aumentano dal centro alla periferia.
		+
		+	[[Image:Ilcielodeinavigatori GNOC.GIF|center]]
		+
		+
		+	La proiezione gnomonica raffigurata è equatoriale e centrografica, puramente geometrica. Non è conforme, nè equidistante, ma le distorsioni sono piccole al centro e crescono alla periferia, dove diventano intollerabili. Ha una proprietà unica: ogni grande circolo risulta essere rettilineo, qualunque sia la sua direzione. Conseguentemente l'equatore e tutti i meridiani sono rettilinei, ma non lo sono i paralleli.
		+
		+	[[Image:Ilcielodeinavigatori ORTHO.GIF|center]]
		+
		+
		+	La proiezione ortografica qui rappresentata è una proiezione obliqua, poichè il piano è tangente alla sfera terrestre non lungo l'equatore, ma lungo un parallelo. In questo tipo di proiezione si hanno poche e trascurabili distorsioni attorno al centro, ma evidenti compressioni quando ci si allontana da esso.
		+
		+
		+	['''Per tornare alla pagina precedente usare il bottone back del browser''']
		+
		+
		+	=Rallentamento della velocità di rotazione della Terra=
		+
		+
		+	Negli anni '30 fu dimostrato che le posizioni apparenti del Sole, della Luna e dei pianeti, calcolate per un'epoca abbastanza lontana, usando come unità di tempo il secondo definito come la 86.400-esima parte del giorno attuale, risultavano sistematicamente spostate ad Ovest, rispetto alle loro posizioni documentate storicamente, in occasione di qualche evento eccezionale come le eclissi di Sole o di Luna. Questo significava che la velocità di rotazione della Terra era, nel passato, maggiore di adesso e che il nostro pianeta stava progressivamente rallentando. Sappiamo che il fenomeno è dovuto principalmente alla dissipazione dell'energia meccanica di rotazione della Terra, attraverso gli attriti che si generano per gli scorrimenti di grande masse liquide e le deformazioni di grandi masse solide, causate dalle maree. Ma le cose non sono semplici, perchè assistiamo ad una variazione del rallentamento in parte periodica, legata alle variazioni stagionali, ed in parte del tutto irregolare e non compresa.
		+	Se ci limitiamo alla componente costante della decelerazione angolare della Terra, sulla base delle osservazioni astronomiche di 2000 anni, si ottiene il valore:
		+
		+
		+
		+	Un fenomeno governato da un numero così piccolo parrebbe del tutto trascurabile, invece i picccoli ritardi si accumolano e producono differenze, tra le posizioni calcolate e le posizioni osservate, misurabili già dopo pochi anni.
		+	Partiamo da un situazione iniziale al tempo  in cui la Terra ha velocità angolare , pari a 360° al giorno. Dopo  giorni, misurati da un orologio perfetto, che batta il secondo uguale alla 86.400-esima parte del giorno iniziale, avremo una velocità
		+
		+
		+
		+	e la Terra avrà ruotato di un angolo  che non contiene un numero intero di angoli giri, cioè di rotazioni complete.
		+
		+
		+
		+	Dopo 36.525 giorni, cioè un secolo, il giorno si è allungato di soli 2 millesimi di secondo, ma la differenza tra l'angolo orario di una qualunque stella, osservato e previsto, sulla base dell'orologio sincronizzato con il giorno di partenza, è già di 36 secondi, più di 548 secondi d'arco. Dopo duemila anni la differenza è di oltre 4 ore, più: di 60° !
		+
		+
		+	1 secolo 2 secoli 4 secoli 6 secoli 8 secoli 10 secoli 15 secoli 20 secoli
		+	36 secondi 2.5 minuti 9.7 minuti 21.9 minuti 38.9 minuti 1.01 ore 2.28 ore 4.06 ore
		+
		+
		+	Altre informazioni su questi argomenti in rete nei seguenti siti:
		+
		+	Time Service Department U.S. Naval Observatory, Washington, DC
		+	Il Tempo di Internet (in italiano)
		+
		+	['''Per tornare alla pagina precedente usare il bottone back del browser''']
		+
		+
		+	=Scale rotazionali=
		+
		+	Il fenomeno più evidente, causato dalla rotazione e dalla rivoluzione della Terra, è l'alternarsi del giorno e della notte. Si tratta di due intervalli di tempo variabili da un giorno all'altro e dipendenti dalla latitudine dell'osservatore, come risulta dalla tabella, in cui l'ora del sorgere e del tramontare del Sole è espressa in tempo civile (TC), segnato dai comuni orologi.
		+
		+	LUOGO DATA ALBA TRAMONTO DURATA
		+	Firenze  1 Ottobre 1998  06:13:46 17:55:13 11h 35m 9s
		+	(43° 45' N)  30 Ottobre 1998  06:49:32 17:07:30 10h 11m 8s
		+	Napoli  1 Ottobre 1998  06:00:50 17:44:24 11h 37m 33s
		+	(40° 52' N) 30 Ottobre 1998  06:32:29 17:00:47 10h 21m 48s
		+
		+	I Greci ed i Romani dividevano in 12 parti uguali l'arco diurno percorso dal Sole, ottenendo così ore di diversa durata a seconda del giorno dell'anno, le ore temporarie. Alla latitudine di Roma l'ora invernale diurna durava circa 45 minuti e l'ora estiva circa 75 (con riferimento, ovviamente, ai nostri attuali minuti). Gli apparecchi usati per misurarle erano il Polos e lo Gnomone. Il Polos è una specie di tazza semisferica sulla quale si proietta l'ombra di uno stilo orizzontale. Durante il giorno il vertice dell'ombra traccia un cammino arcuato che è la proiezione dell'arco diurno percorso dal Sole in cielo. Lo strumento porta incisi i percorsi diurni dell'ombra per alcuni giorni dell'anno, solitamente gli equinozi ed i solstizi. Questi archi sono divisi in parti ugauli da altri archi appartenenti a circoli meridiani convergenti nel piede dello stilo: le linee orarie.
		+
		+	[[Image:Ilcielodeinavigatori POLOS.GIF|center]]
		+
		+
		+	Il Polos della figura è conservato a Roma, in Vaticano. Si riconoscono 11 linee orarie e 7 percorsi diurni, corrispondenti a ciascun mese dell'anno. I mesi simmetrici, rispetto ai solstizi, sono rapprentati dallo stesso percorso, in quanto il Sole assume gli stessi valori di declinazione: Maggio e Luglio, Novembre e Gennaio ecc.
		+
		+
		+	[[Image:Ilcielodeinavigatori GNOMO.GIF|center]]
		+
		+
		+	Con lo Gnomone l'ora temporaria può essere ricavata misurando la lunghezza dell'ombra proiettata. La lunghezza è diversa non solo ad ore diverse dello stesso giorno, ma anche alla stessa ora di giorni diversi, per cui era necessario corredare lo strumento con tabelle di lunghezze, come quelle che troviamo nell' "Opus Agriculturae" dell'agronomo romano Palladio.
		+
		+
		+	HORA LUNGHEZZA
		+	I et XI Pedes XXIX
		+	II et X Pedes XIX
		+	III et IX Pedes XV
		+	IV et VIII Pedes XII
		+	V et VII Pedes X
		+	VI Pedes IX
		+
		+	L'ora VI coincideva con l'ombra più corta della giornata e corrispondeva alla culminazione del Sole, il nostro mezzogiorno.
		+	Entrambi questi strumenti cessavano di funzionare, se trasportati in luoghi a latitudine diversa da quella per la quale erano stati costruiti o calcolati. I Romani, per molto tempo, non ne capirono la teoria e continuarono a lamentarsi che i Polos, accumolati nel foro e provenienti da luoghi diversi, a seguito delle campagne militari, non andavano d'accordo!!
		+
		+	[[Image:Ilcielodeinavigatori ARMILLA.GIF|center]]
		+
		+
		+
		+	Una scala più uniforme venne ottenuta dividendo in 24 parti uguali il tempo che intercorre tra due culminazioni successive del Sole, il giorno solare vero. Le ore così definite sono quasi uguali in tutti i giorni dell'anno ed hanno circa la stessa durata delle nostre. Vennero chiamate ore equinoziali perchè coincidono con le temporarie agli equinozi, quando l'arco diurno del Sole è uguale a quello notturno. Gli strumenti che le misurano sono, da una parte gli astrolabi e le armille utilizzate solo dagli astronomi, e dall'altra le meridiane, veri e propri orologi pubblici che, dalla fine del XV secolo, sono presenti in tutta Europa. Il termine meridiana è errato, sarebbe meglio chiamarli orologi solari perchè solo alcuni di essi sono meridane, cioè quelli che indicano quando il Sole si trova in meridiano. Tuttavia in Italia ed in Toscana in particolare, si usa il termine meridiana per indicare un qualsiasi orologio solare.
		+
		+
		+	[[Image:Ilcielodeinavigatori SUNDIAL.GIF|center]]
		+
		+
		+	Il principio di funzionamento della meridiana era sicuramente noto anche ai tempi di Tolomeo, ma non fu utilizzato, fuori dall'ambito strettamente astronomico, perchè in quelle società le ore uguali non erano richieste. Le ore uguali vengono introdotte negli usi civili dalle società mercantili del basso medioevo, quando il tempo di produzione delle merci viene incorporato, come valore aggiunto, nel loro costo.
		+	Nell'orologio solare la lancetta è data dall'ombra di uno stilo parallelo all'asse della Terra. La direzione dell'ombra di uno stilo parallelo all'asse della Terra, raccolta su una superfice qualsiasi, è sempre la stessa per uguali valori dell'angolo orario del Sole, in qualunque giorno dell'anno.
		+	Ma anche le ore equinoziali non costituiscono una scala uniforme, in quanto il giorno solare vero non è costante, a causa dell' eccentricità dell'orbita terrestre e dell'inclinazione dell'asse di rotazione sul piano orbitale.
		+	Consideriamo a mò di esempio i tempi di culminazione (il mezzogiorno solare vero locale) a Firenze in due giorni del Dicembre 1998.
		+
		+
		+	DATA MEZZOGIORNO VERO TEMPO INTERCORRENTE
		+	1 Dicembre 1998 12:03:59
		+	2 Dicembre 1998 12:04:22 24h 0m 23s
		+	29 Dicembre 1998 12:16:59
		+	30 Dicembre 1998 12:17:28 24h 0m 29
		+
		+	In un giorno vi sono 24 ore, in un'ora 60 minuti ed in un minuto 60 secondi. Quindi in un giorno 60X60X24 = 86.400 secondi. Se definiamo il secondo come la 86.400-esima parte del giorno solare vero, l'unità definita il 1 Dicembre risulterà più corta di quella definita alla fine del mese.
		+	La diversa durata del giorno solare vero era già nota agli astronomi greci che la deducevano dalla diversa durata delle stagioni.
		+
		+
		+
		+	STAGIONE DURATA
		+	Primavera 92g 20.2h
		+	Estate 93g 14.4h
		+	Autunno 89g 18.7h
		+	Inverno 89g 0.5h
		+
		+	Con la rivoluzione industriale esigenze civili e tecnico-scientifiche impongono che il secondo sia rigorosamente costante. Nel 1700 viene introdotto, anche nella vita civile, un artificio astronomico-matematico: il Sole medio. Si tratta di un corpo fittizio che percorre l'equatore celeste con velocità angolare costante, nello stesso tempo in cui il Sole vero percorre l'eclittica. L'angolo orario del sole medio, contato a partire dall'antimeridiano locale, prende il nome di Tempo Solare Medio. Tra tempo solare vero e tempo solare medio vi è una differenza che varia di giorno in giorno, con il sole vero che talvolta segue e talvolta precede il sole medio. Questa differenza prende il nome di Equazione del tempo e può essere calcolata dagli elementi orbitali della Terra, per ogni giorno dell'anno.
		+
		+	Il tempo solare medio è un tempo locale e quindi dipende dalla longitudine dell'osservatore; sono sufficienti pochi chilometri per avere differenze apprezzabili. La tabella dà il tempo solare vero locale (TSVL) e quello medio locale (TSML) per Firenze ed Arezzo, nello stesso istante del 26 Novembre 1998, quando gli orologi segnavano le ore 12:00.
		+
		+
		+	LUOGO TSVL TSML
		+	Arezzo 11:59:38 11:47:00
		+	Firenze 11:57:39 11:45:01
		+
		+	Per ovviare a ciò la Terra è stata divisa in 24 spicchi meridiani chiamati Fusi Orari. Si è definito Tempo Civile di ogni luogo all'interno del fuso, il tempo solare medio, misurato lungo il meridiano centrale del fuso. La differenza tra i tempi locali di due luoghi è pari alla differenza delle loro longitudini, espresse in ore, minuti e secondi di tempo. La tabella indica la differenza di 21 secondi tra i tempi locali di Firenze ed Arezzo. Questo valore deriva dalle loro longitudini; Firenze 11° 15' 19" Est, Arezzo 11° 45' Est.
		+
		+	Per la determinazione delle longitudini e per le osservazioni astronomiche si usa il Tempo Universale (TU), che è il tempo solare medio misurato a Greenwich. L'origine della scala è fissata alla culminazione inferiore (mezzanotte) a Greenwich del sole medio, e l'unità di scala, il secondo, è definita come la 86.400-esima parte del giorno solare medio.
		+
		+	[[Image:Ilcielodeinavigatori PASSAG.GIF|center]]
		+
		+
		+	A dispetto delle definizioni il tempo universale non viene misurato direttamente; non è facile misurare la posizione del Sole con grande precisione, dal momento che non è non è un oggetto puntiforme. Si preferisce determinare (usando particolari canocchiali chiamati strumenti dei passaggi) l'istante esatto della culminazione meridiana di alcune stelle di cui si conoscono, con grande esattezza, le coordinate equatoriali che vengono corrette per la precessione ed altri effetti minori. Alla culminazione l'angolo orario di un corpo celeste è nullo e la sua ascensione retta è uguale al tempo siderale locale. Da questo si ricava poi, con il calcolo, il tempo universale.
		+	Il tempo universale è strettamente legato al tempo siderale e fornisce la posizione della Terra rispetto alla stelle. La sua conoscenza è essenziale in Geofisica, Topografia, Navigazione marittima e spaziale.
		+	Contrariamente al Sole, le stelle sembrano trascinate dal moto regolare della sfera celeste, dovuto a quello di rotazione della Terra. Il tempo che intercorre tra due culminazioni successive di una qualsiasi stella prende il nome di Giorno siderale e, da un giorno all'altro, appare essere assolutamente costante. Per millenni il moto di rotazione apparente della sfera celeste, e per secoli quello reale della Terra, sono stati considerati assolutamente uniformi. Ma non è così: la Terra sta rallentando e la durata del giorno siderale aumenta di due millesimi di secondo ogni 100 anni. Eulero lo sospettò fin dalla fine del XVIII secolo per ragioni teoriche e nel 1936 lo si dimostrò, ricalcolando le date e gli orari di antiche eclissi e confrontando i risultati con le testimonianze storiche. Diverse sono le cause che rendono non uniforme la rotazione della Terra. L'attrito delle maree è il maggior responsabile: una parte dell'energia meccanica della rotazione viene dissipata sotto forma di calore. Spostamenti di grandi masse di acqua e di aria causano variazioni stagionali della sua velocità. A tutto questo si aggiunge poi una variabilità accidentale, talvolta positiva, talvolta negativa.
		+	Non esiste una soddisfacente descrizione quantitativa di tutte queste cause, per cui non è possibile correggere a priori le osservazioni, in modo da rendere uniforme la scala di tempo universale. Per questo motivo l'unità di scala, il secondo di tempo universale, non è più in vigore dal 1956, quando fu sostituito dall'unità di una scala non rotazionale: il secondo del Tempo delle Effemeridi.
		+
		+	Altre informazioni su questi argomenti in rete nei seguenti siti:
		+
		+	Orologi solari Breve storia
		+	Unione Astrofili Italiani - Sezione Quadranti Solari
		+	Information Leaflets Prontuario di astronomia (in inglese)
		+	The National Earth Orientation Service (NEOS) Il servizio U.S.A. che si occupa delle variazioni della rotazione terrestre (in inglese)
		+
		+	['''Per tornare alla pagina precedente usare il bottone back del browser''']

---

Versione delle 09:35, 1 nov 2010

Indice 1 Ottobre 2 Ogigia 3 Paralleli 4 Pitea, esploratore avventuroso (e fantasioso) del IV secolo a.C. 5 Pleiadi 6 La Precessione degli Equinozi 7 Le proiezioni prospettiche 8 Rallentamento della velocità di rotazione della Terra 9 Scale rotazionali

Ottobre

Ottobre: si ara e si semina nei campi.

[Per tornare alla pagina precedente usare il bottone back del browser]

Ogigia

È l'isola del Mediterraneo occidentale in cui, secondo Omero, viveva Calipso. Molto probabilmente si tratta di un luogo immaginario in quanto ogni tentativo di identificazione è risultato inconsistente.

[Per tornare alla pagina precedente usare il bottone back del browser]

Paralleli

La Terra ha una forma molto vicina alla sfera. In una sfera non ci sono punti particolari come sono i vertici per esempio di un cubo, ma se la sfera si mette a ruotare ecco che due punti della sfera assumono una grande importanza sono i poli dell'asse di rotazione. Sono cioè quei due punti, diametralmente opposti, in cui l'asse di rotazione incontra la superficie della sfera. Se consideriamo i piani perpendicolari all'asse di rotazione che intersecano la sfera, vediamo che ognuno di essi taglia la sfera lungo cerchi il cui diametro è tanto più piccolo quanto più il piano è vicino ad un polo della sfera Questi cerchi vengono detti circoli paralleli o paralleli. Il cerchio più grande è detto cerchio equatoriale ed è quello che si ottiene tagliando la sfera con un piano equidistante dai due poli e quindi passante per il suo centro. I paralleli sono tutti Piccoli circoli con esclusione dell'Equatore che è un Grande circolo

[Per tornare alla pagina precedente usare il bottone back del browser]

Pitea, esploratore avventuroso (e fantasioso) del IV secolo a.C.

Pitea, navigatore greco originario della colonia di Massalia (la moderna Marsiglia), fu il primo greco a descrivere la costa nord-occidentale dell'Europa, compresa la Gran Bretagna. Il suo libro principale sull'"Oceano" è stato perduto, tuttavia le sue descrizioni sono state ampiamente copiate dai geografi che sono vissuti dopo di lui, in particolare Eratostene e Posidonio, altri invece come Polibio e Strabone considerarono le sue descrizioni come pure fantasie. Tuttavia, è sicuro che Pitea abbia veramente percorso le coste europee spingendosi molto a Nord; questa certezza deriva dalle descrizioni delle usanze dei popoli incontrati, ma soprattutto dalle indicazioni che Pitea dà sulla lunghezza dell'ombra dello gnomone al solstizio d'Estate a quelle latitudini. Tra le descrizioni di questo avventuroso navigatore greco troviamo anche quelle della lontana Tule, una città che si sarebbe dovuta trovare a sei giorni di navigazione delle coste settentrionali dell'Inghilterra, ed il cui territorio si estendeva verso il circolo polare artico.

[Per tornare alla pagina precedente usare il bottone back del browser]

Pleiadi

L'ammasso delle Pleiadi osservato con un binocolo astronomico Le Pleiadi costituiscono l'ammasso di stelle forse più famoso. Si trovano nella costellazione del Toro a Nord Ovest della stella più luminosa, Aldebran. Ad occhio nudo se ne vedono sette, difatti le Pleiadi sono note anche come le "sette sorelle". Con un buon binocolo, e con il cielo sufficientemente scuro, si scopre che l'ammasso, il cui diametro è all'incirca uguale a quello della Luna, è costituito da centinaia di stelle a cui è associata una debole nebulosità.

La costellazione del Toro da Johann Hevelius: URANOGRAPHIA (1690) (la freccia indica l'ammasso delle Pleiadi). L'immagine appartiene alla collezione storica del Museo astronomico di Brera, disponibile in rete . Nella cartografia celeste dell'epoca i punti cardinali Est ed Ovest risultano invertiti in quanto il cielo viene rappresentato come un globo celeste visto dall'esterno. Queste stelle hanno eccitato la curiosità fino dall'antichità e qualche volta sono state considerate esse stesse una costellazione. Per i Greci esse erano le figlie di Atlante e Pleione, che sono l'ottava e la nona stella del gruppo in ordine di luminosità decrescente. Secondo un'altra leggenda esse erano le compagne di caccia della dea Artemide, che, quando vennero molestate dal brutale cacciatore Orione, furono strappate alla terra dalla loro protettrice e poste in cielo. Spesso nelle leggenda vengono anche indicate come le stelle piangenti. Potrebbero piangere per la scomparsa di una sorella, la stella Sterope, che nel tempo si è molto indebolita e quindi si perde facilmente nell'osservazione ad occhio nudo.

[Per tornare alla pagina precedente usare il bottone back del browser]

La Precessione degli Equinozi

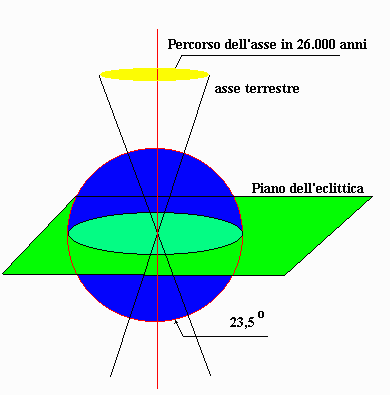
L'attrazione gravitazionale della Luna e del Sole tende a modificare la direzione dell'asse di rotazione terrestre facendole descrivere, in senso orario, la superficie di un cono in poco più di 26.000 anni. L'asse di questo cono è perpendicolare al piano dell'orbita terreste ossia dell'eclittica. Di conseguenza i poli celesti descrivono un cerchio attorno ai corrispondenti poli dell'eclittica, mantenendosi a 23° e 26' da essi. Il piano equatoriale è solidale con l'asse di rotazione, per cui i suoi punti d'intersezione con l'eclittica (chiamati il punto Gamma ed il punto Omega) scorrono lentamente in senso orario, muovendosi di circa 50" all'anno. Gli equinozi (il punto Gamma ed Omega) sembrano precedere le stelle verso il tramonto, da qui il nome di Precessione degli Equinozi che viene dato a questo fenomeno. Il punto Gamma, muovendosi apparentemente in senso orario lungo l'eclittica, va incontro al Sole che si muove, in senso antiorario, sullo stesso piano. Per questo motivo, l'anno tropico è di circa 20 minuti più breve dell'anno sidereo. L'anno tropico dura 365.2422 giorni, ovvero 365g 5h 49m, mentre l'anno sidereo 365.253 ovvero 365g 6h 9m. Il fenomeno della Precessione, modificando la posizione dell'Equinozio di Primavera rispetto alle stelle, comporta il cambiamento sia dell'ascensione retta che della declinazione. La Precessione degli Equinozi non ha praticamente alcun effetto sul pianeta Terra, in quanto lascia invariata l'inclinazione dell'eclittica, da cui dipende l'ampiezza della variazione stagionale dell'inclinazione dei raggi solari, che scaldano il suolo terrestre. La manifestazione più evidente della Precessione è lo spostamento del Polo Nord Celeste tra le stelle e quindi l'avvicendamento, nel tempo, delle stelle polari, cioè delle stelle luminose che, di volta in volta, risultano più vicine ad esso. Nelle cartine seguenti la lettera P indica il polo nord celeste.

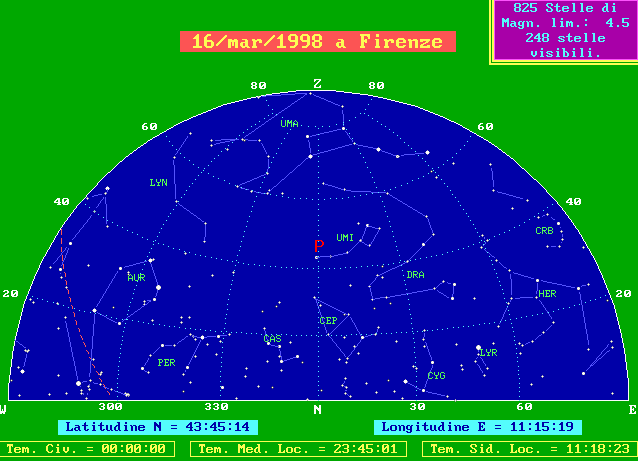
Il cielo a Firenze a meta' di Aprile del 1998 La Polare attuale è la stella alfa Ursae Minoris (UMI), ma 2500 anni fa era Kosciab, la beta della stessa costellazione.

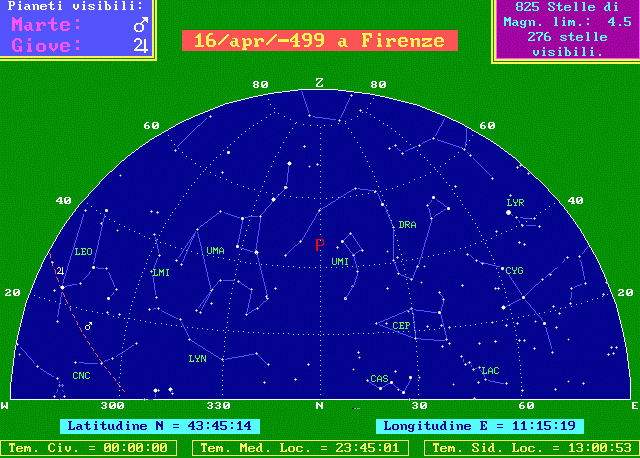
Il cielo a Firenze a metà di Aprile di 2500 anni fa e sarà la stella Vega, l'alfa della Lira (LYR) tra 11.000 anni

Il cielo a Firenze a metà di Aprile tra 11.000 anni Dalla variazione delle coordinate equatoriali delle stelle al passare del tempo, deriva anche che le stelle circumpolari (quelle che non sorgono nè tramontano in un dato luogo) possono diventare occidue (quelle che sorgono e tramontano) e le stelle occidue diventare invisibili (quelle che non sorgono mai) e viceversa.

Altre informazioni sulla precessione in rete nei seguenti siti:

Dimostrazione della Precessione nel laboratorio di Fisica Precession of the Equinoxes Una spiegazione completa, ma con tanta matematica Il mito di Mitra spiegato con la precessione.

[Per tornare alla pagina precedente usare il bottone back del browser]

Le proiezioni prospettiche

Le proiezioni prospettiche si distinguono in proiezioni polari, equatoriali o qualsiasi, a seconda che il polo di proiezione (punto di tangenza della sfera con il piano di proiezione) sia uno dei poli terrestri o si trovi sull'equatore o coincida con un punto qualsiasi della superficie terrestre. In ciascuno dei casi la proiezione potrà essere centrografica, stereografica, od ortografica, a seconda della posizione del punto vista. Nella proiezione centrografica, il punto di vista è al centro della sfera, in quella stereografica è nel punto diametralmente opposto al polo di proiezione, mentre in quella ortografica si trova all'infinito.

Nella pratica cartografica si rivelano molto più utili le proiezioni azimutali modificate, in modo da conservare, con opportuni algoritmi, alcune o tutte le proprietà cartografiche. Alcuni esempi:

La proiezione azimutale equidistante raffigurata è una proiezione polare, centrografica modificata. I meridiani sono rettilinei, i paralleli concentrici e volutamente ed arbitrariamente equidistanziati. In questo modo l'equidistanza è assicurata lungo ogni direzione a partire dal centro che, in questo caso, coincide con il polo geografico, essendo l'asse terrestre perpendicolare al piano di proiezione. Le lossodromiche che si irradiano dal centro coincidono con i meridiani e sono quindi rettilinee.

Anche in questo caso la proiezione e' polare, centrografica e modificata. La modifica consiste nel garantire l'equivalenza delle superfici. In questa proiezione i paralleli non sono equidistanziati e tendono ad avvicinarsi verso la periferia della carta.

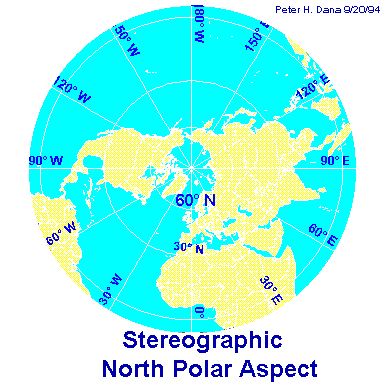
La proiezione stereografica è una proiezione puramente geometrica, non modificata. Quella raffigurata è polare con il punto di vista nel Polo Sud geografico. Nella proiezione stereografica gli angoli compresi tra due circoli sulla sfera vengono conservati sulla carta. quindi la proiezione è isogonica e conforme: i continenti mantengono la loro forma. Questo non è però vero per le aree, che aumentano dal centro alla periferia.

La proiezione gnomonica raffigurata è equatoriale e centrografica, puramente geometrica. Non è conforme, nè equidistante, ma le distorsioni sono piccole al centro e crescono alla periferia, dove diventano intollerabili. Ha una proprietà unica: ogni grande circolo risulta essere rettilineo, qualunque sia la sua direzione. Conseguentemente l'equatore e tutti i meridiani sono rettilinei, ma non lo sono i paralleli.

La proiezione ortografica qui rappresentata è una proiezione obliqua, poichè il piano è tangente alla sfera terrestre non lungo l'equatore, ma lungo un parallelo. In questo tipo di proiezione si hanno poche e trascurabili distorsioni attorno al centro, ma evidenti compressioni quando ci si allontana da esso.

[Per tornare alla pagina precedente usare il bottone back del browser]

Rallentamento della velocità di rotazione della Terra

Negli anni '30 fu dimostrato che le posizioni apparenti del Sole, della Luna e dei pianeti, calcolate per un'epoca abbastanza lontana, usando come unità di tempo il secondo definito come la 86.400-esima parte del giorno attuale, risultavano sistematicamente spostate ad Ovest, rispetto alle loro posizioni documentate storicamente, in occasione di qualche evento eccezionale come le eclissi di Sole o di Luna. Questo significava che la velocità di rotazione della Terra era, nel passato, maggiore di adesso e che il nostro pianeta stava progressivamente rallentando. Sappiamo che il fenomeno è dovuto principalmente alla dissipazione dell'energia meccanica di rotazione della Terra, attraverso gli attriti che si generano per gli scorrimenti di grande masse liquide e le deformazioni di grandi masse solide, causate dalle maree. Ma le cose non sono semplici, perchè assistiamo ad una variazione del rallentamento in parte periodica, legata alle variazioni stagionali, ed in parte del tutto irregolare e non compresa. Se ci limitiamo alla componente costante della decelerazione angolare della Terra, sulla base delle osservazioni astronomiche di 2000 anni, si ottiene il valore:

Un fenomeno governato da un numero così piccolo parrebbe del tutto trascurabile, invece i picccoli ritardi si accumolano e producono differenze, tra le posizioni calcolate e le posizioni osservate, misurabili già dopo pochi anni. Partiamo da un situazione iniziale al tempo in cui la Terra ha velocità angolare , pari a 360° al giorno. Dopo giorni, misurati da un orologio perfetto, che batta il secondo uguale alla 86.400-esima parte del giorno iniziale, avremo una velocità

e la Terra avrà ruotato di un angolo che non contiene un numero intero di angoli giri, cioè di rotazioni complete.

Dopo 36.525 giorni, cioè un secolo, il giorno si è allungato di soli 2 millesimi di secondo, ma la differenza tra l'angolo orario di una qualunque stella, osservato e previsto, sulla base dell'orologio sincronizzato con il giorno di partenza, è già di 36 secondi, più di 548 secondi d'arco. Dopo duemila anni la differenza è di oltre 4 ore, più: di 60° !

1 secolo 2 secoli 4 secoli 6 secoli 8 secoli 10 secoli 15 secoli 20 secoli 36 secondi 2.5 minuti 9.7 minuti 21.9 minuti 38.9 minuti 1.01 ore 2.28 ore 4.06 ore

Altre informazioni su questi argomenti in rete nei seguenti siti:

Time Service Department U.S. Naval Observatory, Washington, DC Il Tempo di Internet (in italiano)

[Per tornare alla pagina precedente usare il bottone back del browser]

Scale rotazionali

Il fenomeno più evidente, causato dalla rotazione e dalla rivoluzione della Terra, è l'alternarsi del giorno e della notte. Si tratta di due intervalli di tempo variabili da un giorno all'altro e dipendenti dalla latitudine dell'osservatore, come risulta dalla tabella, in cui l'ora del sorgere e del tramontare del Sole è espressa in tempo civile (TC), segnato dai comuni orologi.

LUOGO DATA ALBA TRAMONTO DURATA Firenze 1 Ottobre 1998 06:13:46 17:55:13 11h 35m 9s (43° 45' N) 30 Ottobre 1998 06:49:32 17:07:30 10h 11m 8s Napoli 1 Ottobre 1998 06:00:50 17:44:24 11h 37m 33s (40° 52' N) 30 Ottobre 1998 06:32:29 17:00:47 10h 21m 48s

I Greci ed i Romani dividevano in 12 parti uguali l'arco diurno percorso dal Sole, ottenendo così ore di diversa durata a seconda del giorno dell'anno, le ore temporarie. Alla latitudine di Roma l'ora invernale diurna durava circa 45 minuti e l'ora estiva circa 75 (con riferimento, ovviamente, ai nostri attuali minuti). Gli apparecchi usati per misurarle erano il Polos e lo Gnomone. Il Polos è una specie di tazza semisferica sulla quale si proietta l'ombra di uno stilo orizzontale. Durante il giorno il vertice dell'ombra traccia un cammino arcuato che è la proiezione dell'arco diurno percorso dal Sole in cielo. Lo strumento porta incisi i percorsi diurni dell'ombra per alcuni giorni dell'anno, solitamente gli equinozi ed i solstizi. Questi archi sono divisi in parti ugauli da altri archi appartenenti a circoli meridiani convergenti nel piede dello stilo: le linee orarie.

Il Polos della figura è conservato a Roma, in Vaticano. Si riconoscono 11 linee orarie e 7 percorsi diurni, corrispondenti a ciascun mese dell'anno. I mesi simmetrici, rispetto ai solstizi, sono rapprentati dallo stesso percorso, in quanto il Sole assume gli stessi valori di declinazione: Maggio e Luglio, Novembre e Gennaio ecc.

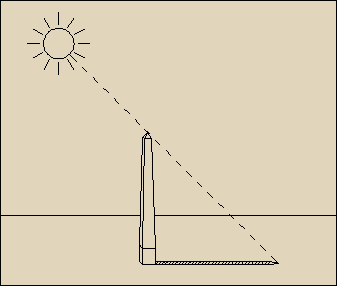
Con lo Gnomone l'ora temporaria può essere ricavata misurando la lunghezza dell'ombra proiettata. La lunghezza è diversa non solo ad ore diverse dello stesso giorno, ma anche alla stessa ora di giorni diversi, per cui era necessario corredare lo strumento con tabelle di lunghezze, come quelle che troviamo nell' "Opus Agriculturae" dell'agronomo romano Palladio.

HORA LUNGHEZZA I et XI Pedes XXIX II et X Pedes XIX III et IX Pedes XV IV et VIII Pedes XII V et VII Pedes X VI Pedes IX

L'ora VI coincideva con l'ombra più corta della giornata e corrispondeva alla culminazione del Sole, il nostro mezzogiorno. Entrambi questi strumenti cessavano di funzionare, se trasportati in luoghi a latitudine diversa da quella per la quale erano stati costruiti o calcolati. I Romani, per molto tempo, non ne capirono la teoria e continuarono a lamentarsi che i Polos, accumolati nel foro e provenienti da luoghi diversi, a seguito delle campagne militari, non andavano d'accordo!!

Una scala più uniforme venne ottenuta dividendo in 24 parti uguali il tempo che intercorre tra due culminazioni successive del Sole, il giorno solare vero. Le ore così definite sono quasi uguali in tutti i giorni dell'anno ed hanno circa la stessa durata delle nostre. Vennero chiamate ore equinoziali perchè coincidono con le temporarie agli equinozi, quando l'arco diurno del Sole è uguale a quello notturno. Gli strumenti che le misurano sono, da una parte gli astrolabi e le armille utilizzate solo dagli astronomi, e dall'altra le meridiane, veri e propri orologi pubblici che, dalla fine del XV secolo, sono presenti in tutta Europa. Il termine meridiana è errato, sarebbe meglio chiamarli orologi solari perchè solo alcuni di essi sono meridane, cioè quelli che indicano quando il Sole si trova in meridiano. Tuttavia in Italia ed in Toscana in particolare, si usa il termine meridiana per indicare un qualsiasi orologio solare.

Il principio di funzionamento della meridiana era sicuramente noto anche ai tempi di Tolomeo, ma non fu utilizzato, fuori dall'ambito strettamente astronomico, perchè in quelle società le ore uguali non erano richieste. Le ore uguali vengono introdotte negli usi civili dalle società mercantili del basso medioevo, quando il tempo di produzione delle merci viene incorporato, come valore aggiunto, nel loro costo. Nell'orologio solare la lancetta è data dall'ombra di uno stilo parallelo all'asse della Terra. La direzione dell'ombra di uno stilo parallelo all'asse della Terra, raccolta su una superfice qualsiasi, è sempre la stessa per uguali valori dell'angolo orario del Sole, in qualunque giorno dell'anno. Ma anche le ore equinoziali non costituiscono una scala uniforme, in quanto il giorno solare vero non è costante, a causa dell' eccentricità dell'orbita terrestre e dell'inclinazione dell'asse di rotazione sul piano orbitale. Consideriamo a mò di esempio i tempi di culminazione (il mezzogiorno solare vero locale) a Firenze in due giorni del Dicembre 1998.

DATA MEZZOGIORNO VERO TEMPO INTERCORRENTE 1 Dicembre 1998 12:03:59 2 Dicembre 1998 12:04:22 24h 0m 23s 29 Dicembre 1998 12:16:59 30 Dicembre 1998 12:17:28 24h 0m 29

In un giorno vi sono 24 ore, in un'ora 60 minuti ed in un minuto 60 secondi. Quindi in un giorno 60X60X24 = 86.400 secondi. Se definiamo il secondo come la 86.400-esima parte del giorno solare vero, l'unità definita il 1 Dicembre risulterà più corta di quella definita alla fine del mese. La diversa durata del giorno solare vero era già nota agli astronomi greci che la deducevano dalla diversa durata delle stagioni.

STAGIONE DURATA Primavera 92g 20.2h Estate 93g 14.4h Autunno 89g 18.7h Inverno 89g 0.5h

Con la rivoluzione industriale esigenze civili e tecnico-scientifiche impongono che il secondo sia rigorosamente costante. Nel 1700 viene introdotto, anche nella vita civile, un artificio astronomico-matematico: il Sole medio. Si tratta di un corpo fittizio che percorre l'equatore celeste con velocità angolare costante, nello stesso tempo in cui il Sole vero percorre l'eclittica. L'angolo orario del sole medio, contato a partire dall'antimeridiano locale, prende il nome di Tempo Solare Medio. Tra tempo solare vero e tempo solare medio vi è una differenza che varia di giorno in giorno, con il sole vero che talvolta segue e talvolta precede il sole medio. Questa differenza prende il nome di Equazione del tempo e può essere calcolata dagli elementi orbitali della Terra, per ogni giorno dell'anno.

Il tempo solare medio è un tempo locale e quindi dipende dalla longitudine dell'osservatore; sono sufficienti pochi chilometri per avere differenze apprezzabili. La tabella dà il tempo solare vero locale (TSVL) e quello medio locale (TSML) per Firenze ed Arezzo, nello stesso istante del 26 Novembre 1998, quando gli orologi segnavano le ore 12:00.

LUOGO TSVL TSML Arezzo 11:59:38 11:47:00 Firenze 11:57:39 11:45:01

Per ovviare a ciò la Terra è stata divisa in 24 spicchi meridiani chiamati Fusi Orari. Si è definito Tempo Civile di ogni luogo all'interno del fuso, il tempo solare medio, misurato lungo il meridiano centrale del fuso. La differenza tra i tempi locali di due luoghi è pari alla differenza delle loro longitudini, espresse in ore, minuti e secondi di tempo. La tabella indica la differenza di 21 secondi tra i tempi locali di Firenze ed Arezzo. Questo valore deriva dalle loro longitudini; Firenze 11° 15' 19" Est, Arezzo 11° 45' Est.

Per la determinazione delle longitudini e per le osservazioni astronomiche si usa il Tempo Universale (TU), che è il tempo solare medio misurato a Greenwich. L'origine della scala è fissata alla culminazione inferiore (mezzanotte) a Greenwich del sole medio, e l'unità di scala, il secondo, è definita come la 86.400-esima parte del giorno solare medio.

A dispetto delle definizioni il tempo universale non viene misurato direttamente; non è facile misurare la posizione del Sole con grande precisione, dal momento che non è non è un oggetto puntiforme. Si preferisce determinare (usando particolari canocchiali chiamati strumenti dei passaggi) l'istante esatto della culminazione meridiana di alcune stelle di cui si conoscono, con grande esattezza, le coordinate equatoriali che vengono corrette per la precessione ed altri effetti minori. Alla culminazione l'angolo orario di un corpo celeste è nullo e la sua ascensione retta è uguale al tempo siderale locale. Da questo si ricava poi, con il calcolo, il tempo universale. Il tempo universale è strettamente legato al tempo siderale e fornisce la posizione della Terra rispetto alla stelle. La sua conoscenza è essenziale in Geofisica, Topografia, Navigazione marittima e spaziale. Contrariamente al Sole, le stelle sembrano trascinate dal moto regolare della sfera celeste, dovuto a quello di rotazione della Terra. Il tempo che intercorre tra due culminazioni successive di una qualsiasi stella prende il nome di Giorno siderale e, da un giorno all'altro, appare essere assolutamente costante. Per millenni il moto di rotazione apparente della sfera celeste, e per secoli quello reale della Terra, sono stati considerati assolutamente uniformi. Ma non è così: la Terra sta rallentando e la durata del giorno siderale aumenta di due millesimi di secondo ogni 100 anni. Eulero lo sospettò fin dalla fine del XVIII secolo per ragioni teoriche e nel 1936 lo si dimostrò, ricalcolando le date e gli orari di antiche eclissi e confrontando i risultati con le testimonianze storiche. Diverse sono le cause che rendono non uniforme la rotazione della Terra. L'attrito delle maree è il maggior responsabile: una parte dell'energia meccanica della rotazione viene dissipata sotto forma di calore. Spostamenti di grandi masse di acqua e di aria causano variazioni stagionali della sua velocità. A tutto questo si aggiunge poi una variabilità accidentale, talvolta positiva, talvolta negativa. Non esiste una soddisfacente descrizione quantitativa di tutte queste cause, per cui non è possibile correggere a priori le osservazioni, in modo da rendere uniforme la scala di tempo universale. Per questo motivo l'unità di scala, il secondo di tempo universale, non è più in vigore dal 1956, quando fu sostituito dall'unità di una scala non rotazionale: il secondo del Tempo delle Effemeridi.

Altre informazioni su questi argomenti in rete nei seguenti siti:

Orologi solari Breve storia Unione Astrofili Italiani - Sezione Quadranti Solari Information Leaflets Prontuario di astronomia (in inglese) The National Earth Orientation Service (NEOS) Il servizio U.S.A. che si occupa delle variazioni della rotazione terrestre (in inglese)

[Per tornare alla pagina precedente usare il bottone back del browser]