Il cielo dei navigatori - Note 3
Da Commissione Divulgazione - Unione Astrofili Italiani.
| Riga 104: | Riga 104: | ||
<br> Il nostro amico vede, a Sud, per lo più le stesse stelle che vediamo noi, ma più alte; per esempio le tre stelle allineate della cintura di Orione (ORI) sono a poco più di 40° a Firenze e salgono a 60° in Libia. Vede però anche una stella che noi non vediamo mai: la brillante Canopo, tra la costellazione della Poppa (PUP) e quella del Pittore (PIC). | <br> Il nostro amico vede, a Sud, per lo più le stesse stelle che vediamo noi, ma più alte; per esempio le tre stelle allineate della cintura di Orione (ORI) sono a poco più di 40° a Firenze e salgono a 60° in Libia. Vede però anche una stella che noi non vediamo mai: la brillante Canopo, tra la costellazione della Poppa (PUP) e quella del Pittore (PIC). | ||
| + | |||
| + | |||
[[Image:Ilcielodeinavigatori FIN22.GIF|center]] | [[Image:Ilcielodeinavigatori FIN22.GIF|center]] | ||
| Riga 115: | Riga 117: | ||
[[Image:Ilcielodeinavigatori FIS23.GIF|center]] | [[Image:Ilcielodeinavigatori FIS23.GIF|center]] | ||
| - | <br> Concentriamoci sulla costellazione dello Scorpione (SCO): a Firenze essa si trova immediatamente ad Est del meridiano. <br> <br> | + | <br> Concentriamoci sulla costellazione dello Scorpione (SCO): a Firenze essa si trova immediatamente ad Est del meridiano. <br> <br> |
[[Image:Ilcielodeinavigatori BU.GIF|center]] | [[Image:Ilcielodeinavigatori BU.GIF|center]] | ||
Versione delle 22:06, 28 nov 2010
AL-IDRISI
Abu Abdallah Muhammad Ibn Muhammad Ibn AbdallahIbn Idris al-Qurtubi al-Hasani nacque a Ceuta, in Spagna nel 1099 a.C. Fu educato a Cordoba e, dopo un lungo periodo di viaggi, si stabilì alla corte normanna di Palermo. La data della sua morte è controversa, potrebbe essere tanto il 1166 quanto il 1180. Le circostanze che lo portarono al servizio del re normanno Ruggero II non sono affatto chiare, i biografi arabi lo considerarono un rinnegato. Il suo contributo principale alla scienza fu nel campo della botanica, con particolare riferimento alle piante medicinali. Anche nella geografia il suo contributo fu però interessante, sappiamo che costruì per il suo sovrano un planisfero in argento e descrisse le terre conosciute in un libro intitolato "il libro di Ruggero" che, in sostanza, è un'enciclopedia geografica in cui si possono trovare informazioni sull'Asia, sull'Africa e sulle terre occidentali. Dopo il successo di questo libro, al-Idrisi volle ampliarlo e lo ripubblicò col titolo "Piacere degli uomini e diletto delle anime". I suoi libri di geografia furono molto letti, in versione latina, nei secoli successivi per la loro chiarezza e la loro semplicità.
[Per tornare alla pagina precedente usare il bottone back del browser]
Gennaio
Gennaio: il mese in cui si fanno i regali.
[Per tornare alla pagina precedente usare il bottone back del browser]
Luglio
Luglio: si miete il grano e si taglia la lana alle pecore.
[Per tornare alla pagina precedente usare il bottone back del browser]
Giugno
Giugno: tutti insieme i contadini tagliano e raccolgono il fieno. In questo mese inizia l'estate, controllate la data...
[Per tornare alla pagina precedente usare il bottone back del browser]
Lamo
Città che si trova nelle zone settentrionali della Terra. Infatti Omero ci indica che in quelle terre un pastore insonne, potrebbe ottenere due paghe, una per il giorno e un'altra per la notte che è luminosa.
[Per tornare alla pagina precedente usare il bottone back del browser]
LEAP SECOND ALERT!
U.S. NAVAL OBSERVATORY
WASHINGTON, D.C. 20392-5420
July 23, 1998
No. 64
TIME SERVICE ANNOUNCEMENT SERIES 14
UTC TIME STEP
1. The International Earth Rotation Service (IERS) has announced the introduction of a time step to occur at the end of December, 1998. 2. Coordinated Universal Time (UTC) will be retarded by 1.0s so that the sequence of dates of the UTC markers will be:
1998 December 31 23h 59m 59s
1998 December 31 23h 59m 60s
1999 January 01 0h 0m 0s
3. The difference between UTC and International Atomic Time (TAI) is: from 1997 01 Jul, UTC to 1999 01 January, UTC: TAI-UTC= +31s from 1999 01 Jan, UTC until further notice: TAI-UTC= +32s 4. The insertion of one leap second will be evident by the change of sign of the DUT1 correction which will become positive. Extrapolated values of DUT1 are distributed weekly in the IERS Bulletin A. 5. All coordinated time scales will be affected by this adjustment. However, Loran-C and GPS will not be adjusted physically. Times of Coincidence for LORAN-C are available on the Time Service Web Page (http://tycho.usno.navy.mil/loran.html). For GPS, the leap second correction contained within the UTC data of subframe 4, page 18 of the navigation message transmitted by satellites will change.
Before the leap second
GPS-UTC = +12 (i.e., GPS is ahead of UTC by twelve seconds)
After the leap second
GPS-UTC = +13s (i.e., GPS will be ahead by thirteen seconds)
DENNIS D. McCARTHY
Director
Directorate of Time
Time Service Dept., U.S. Naval Observatory, Washington, DC
[Per tornare alla pagina precedente usare il bottone back del browser]
Le coordinate geografiche
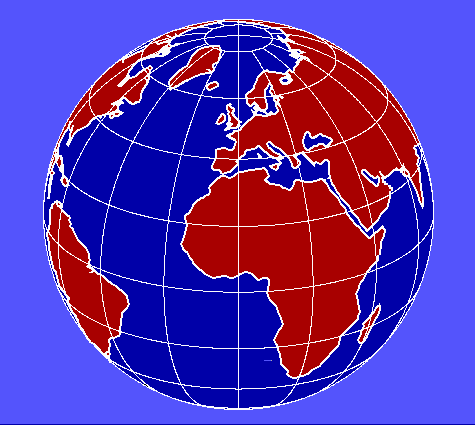
Avvolgiamo la Terra in un reticolato di circoli Paralleli all'Equatore e di circoli Meridiani, convergenti nei Poli. Possiamo infittire il reticolato a piacere, perciò ogni punto si trova all'intersezione di un parallelo con un meridiano e ad esso corrisponde una coppia di numeri: le sue coordinate geografiche, la latitudine e la longitudine.
Latitudine
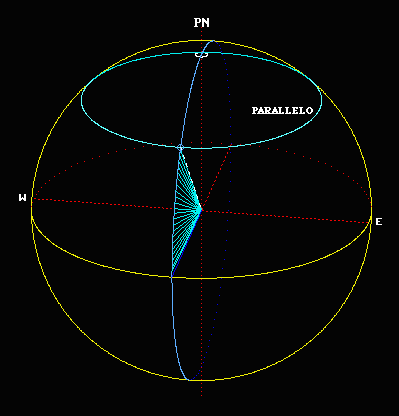
Si definisce latitudine di un luogo della Terra, l'angolo compreso tra il raggio terrestre che passa per quel luogo e il piano dell'Equatore. Tutti i luoghi che hanno la stessa latitudine stanno sullo stesso parallelo.
Longitudine
Si definisce longitudine di un luogo l'angolo diedro compreso tra il piano del meridiano di riferimento ed il piano del meridiano del luogo. Storicamente sono stati assunti quali meridiani di riferimento i meridiani passanti per vari luoghi. Da circa 200 anni il meridiano di riferimento per tutti gli abitanti della Terra è quello passante per l'Osservatorio di Greenwich in Inghilterra. Tutti i luoghi che si trovano sullo stesso meridiano hanno la stessa longitudine.
[Per tornare alla pagina precedente usare il bottone back del browser]
Il cielo è diverso se osservato da luoghi diversi della Terra
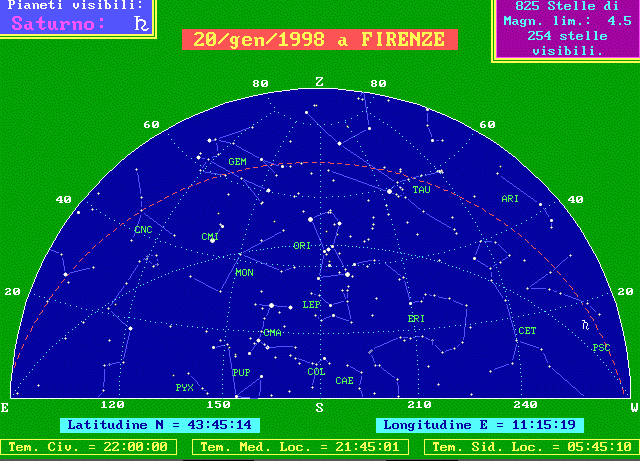
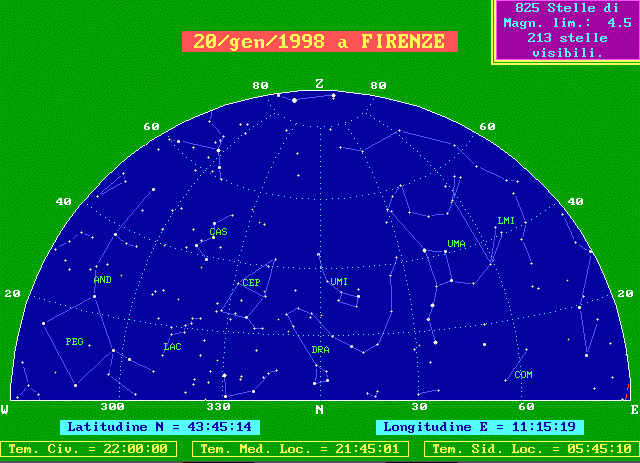
Già gli antichi Greci sapevano che, navigando verso Sud o verso Nord nel Meditteraneo, il cielo visibile cambia, le stelle assumono altezze e direzioni diverse e stelle mai visibili da un luogo diventano visibili da un altro. Da tutto ciò essi avevano correttamente dedotto la curvatura del nostro pianeta, almeno in senso Nord-Sud. Immaginiamo una bella notte invernale; telefoniamo ad un nostro amico che si trovi sul nostro stesso meridiano (quindi con la nostra stessa longitudine ), ma ad una latitudine più bassa, per esempio sulle coste della Libia. Immaginiamo di chiedergli di descriverci il cielo che vede sia verso Sud, sia verso Nord e confrontiamolo con ciò che vediamo noi. (Se avete qualche difficoltà usate le istruzioni per comprendere e leggere le seguenti cartine del cielo).
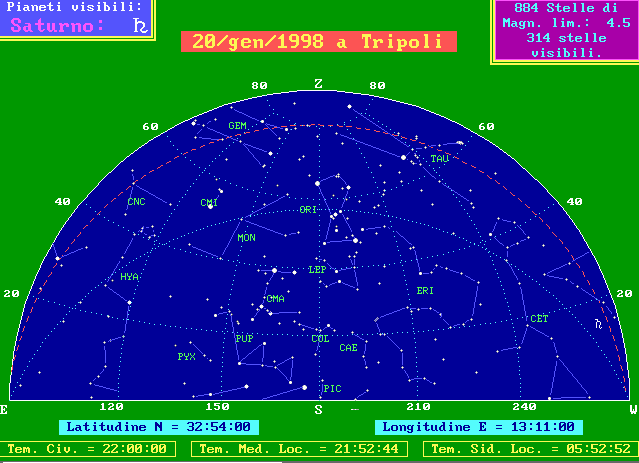
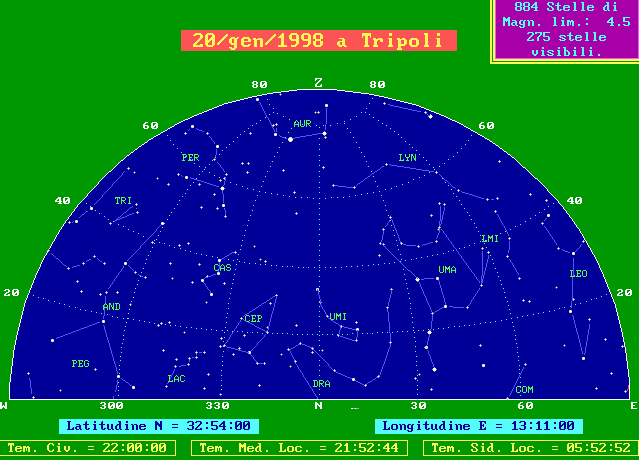
Il nostro amico vede, a Sud, per lo più le stesse stelle che vediamo noi, ma più alte; per esempio le tre stelle allineate della cintura di Orione (ORI) sono a poco più di 40° a Firenze e salgono a 60° in Libia. Vede però anche una stella che noi non vediamo mai: la brillante Canopo, tra la costellazione della Poppa (PUP) e quella del Pittore (PIC).
Verso Nord spicca la diversa altezza delle costellazioni circumpolari e della stella polare che appartiene all'Orsa Minore (UMI) e si trova sulla verticale del punto Nord dell'orizzonte. Gli antichi Greci si resero conto che il cielo è diverso anche se osservato in luoghi a diversa longitudine e dedussero così la curvatura della Terra anche in senso Est-Ovest. Per far ciò usarono le eclissi di Luna che permettono di sincronizzare l'osservazione fatta in luoghi lontani. Noi immaginiamo di telefonare ad un nostro amico che si trova, per esempio a Bucarest (quasi la stessa latitudine di Firenze, ma diversa longitudine) e di chiedergli di descriverci il cielo che vede, in modo da paragonare la sua descrizione con ciò che, nello stesso momento, stiamo vedendo.
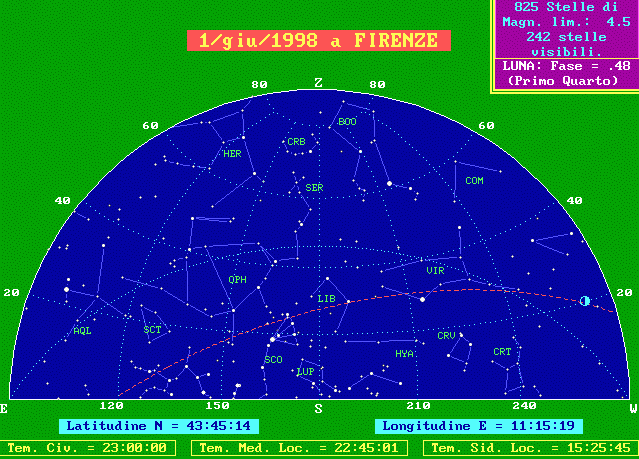
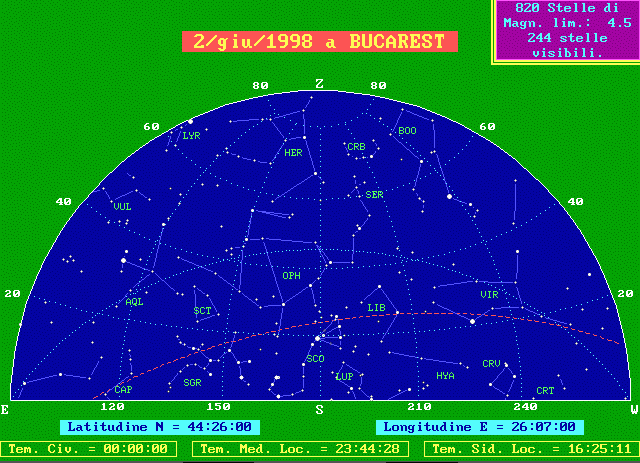
Concentriamoci sulla costellazione dello Scorpione (SCO): a Firenze essa si trova immediatamente ad Est del meridiano.
Il nostro amico la vede invece spostata ad Ovest, mentre sta transitando sul meridiano. Notate che a Bucarest il tempo civile è avanti di un'ora rispetto a Firenze.
[Per tornare alla pagina precedente usare il bottone back del browser]
Marzo
Marzo: in questo mese si collocano i primi lavori agricoli dell'anno, dopo la pausa dell'inverno. Notate la data di passaggio tra il segno dei Pesci e quello dell'Ariete che segnava l'inizio della Primavera.
[Per tornare alla pagina precedente usare il bottone back del browser]
Maggio
Maggio: si celebra la bella stagione con una processione di ragazzi e ragazze che indossano abiti bordati di verde, "livrée de mai", la livrea di maggio. Un'usanza diffusa in tutta Europa.
[Per tornare alla pagina precedente usare il bottone back del browser]
Meridiani
La Terra ha una forma molto vicina alla sfera. In una sfera non ci sono punti particolari come sono i vertici, per esempio, di un cubo, ma se la sfera si mette a ruotare ecco che due punti della sfera assumono una grande importanza sono i poli dell'asse di rotazione. Sono cioè quei due punti, diametralmente opposti, in cui l'asse di rotazione incontra la superficie della sfera. Se consideriamo i piani che passano per l'asse di rotazione, vediamo che ognuno di essi taglia la sfera in spicchi. Si sbucci un'arancia per rendersene conto. Un qualsiasi cerchio ottenuto tagliando la sfera con un piano passante per l'asse di rotazione prende il nome di circolo meridiano o meridiano. Diversamente dai paralleli, i circoli meridiani sono tutti Grandi circoli ed uguali al Circolo equatoriale. Sulla Terra questo non è esattemente vero in quanto il nostro pianeta è leggermente schiacciato ed il diametro equatoriale è più lungo di circa 70 chilometri di quello polare.
[Per tornare alla pagina precedente usare il bottone back del browser]
Il Notturnale
Con il nome di Notturnale o Notturlabio o orologio notturno viene indicato uno strumento astronomico, usato per la misura del tempo mediante l'osservazione della stella polare e della posizione, rispetto ad essa, di due brillanti stelle dell'Orsa Maggiore. La costruzione di strumenti di questo tipo risale al XIII secolo.
Il Notturnale di Della Volpaia conservato presso l'Istituto e Museo di Storia della Scienza di Firenze L'orologio notturno ed in particolare quello rappresentato in figura è costituito tre dischi di ottone che possono ruotare l'uno rispetto all'altro attorno ad un anello centrale. Sporgente da questi tre dischi è un'asta o alidada, sporgente dal bordo del disco più grande, anch'essa libera di ruotare intorno all'anello ed indicante con lo spigolo rettilineo, tutte le possibili rette uscenti dal comune centro di rotazione.
Espoloso del Notturnale di Della Volpaia Lo strumento veniva puntato verso la stella polare che doveva essere traguardata attraverso il foro centrale, dopo aver impostato la data del giorno di osservazione. Il regolo mobile veniva ruotato fino a sovrapporsi con la congiungente le due stelle del Grande Carro, Dhube e Merak. Su i due dischi più interni venivano quindi lette le ore trascorse dalla mezzanotte e quelle trascorse dal tramnoto del giorno precedente. Questo tipo di strumenti, in mano ad un osservatore esperto poteva raggiungere l'accuratezza di 10 minuti.
Per meglio comprendere il funzionamento e l'uso dello strumento vi proponiamo di costruirvene uno, nell'ambito di un'esperienza didattica.
[Per tornare alla pagina precedente usare il bottone back del browser]
L'orologio notturno per la longitudine di Firenze (può funzionare in qualunque luogo)
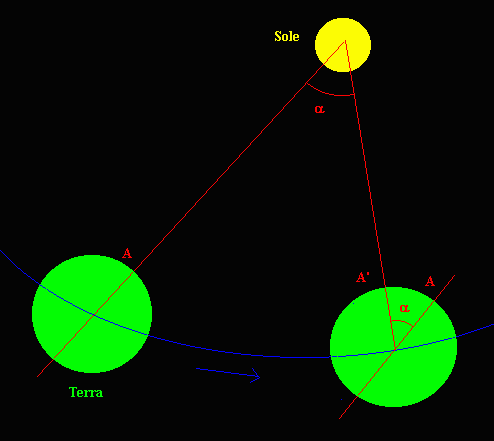
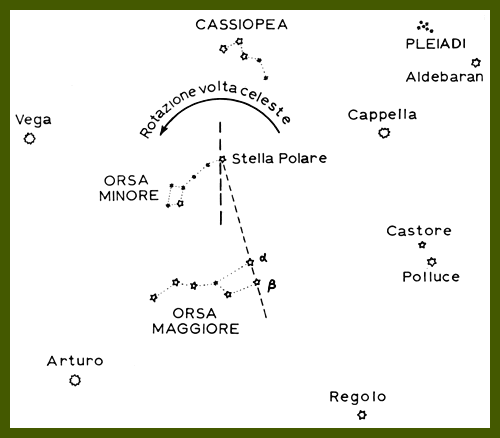
A causa dei movimenti di rotazione e rivoluzione della Terra, l'aspetto del cielo notturno è diverso ad ore diverse dello stesso giorno ed alla stessa ora di giorni diversi. Le stelle vicine alla Polare, cioè alla direzione dell'asse terrestre, sono sempre visibili ad ogni ora di ogni notte dell'anno: dalla loro posizione possiamo facilmente dedurre l'ora o la data. In particolare le due stelle posteriori del "Grande Carro", Dubhe e Merak, risultano, almeno ad occhio nudo, allineate con la Polare e formano la lancetta delle ore di un grande orologio celeste. La lancetta compie un giro completo in 23 ore e 56 minuti, il tempo necessario alla Terra per ruotare di 360°, mentre il Sole, su cui regoliamo i nostri orologi, compie un giro completo in 24 ore.
La ragione di ciò è dovuta alla piccola distanza del Sole, relativamente alle stelle, per cui la Terra deve ruotare per circa 361° per riavere, il giorno dopo, il Sole nella stessa direzione, compensando così il suo spostamento orbitale. Il fenomeno è, in realtà, un po' più complicato perchè la Terra percorre intorno al Sole un'orbita ellittica a velocità variabile ed il suo asse è inclinato di circa 66° sul piano orbitale. Per questo motivo il tempo dell'orologio non è strettamente legato alla posizione del Sole Vero, il cui moto apparente è del tutto irregolare, ma alla Posizione del Sole Medio il cui moto è uniforme e che quindi ritorna, ogni giorno, nella stessa direzione dopo 24 ore esatte. Il nostro precedente ragionamento e la prima figura si riferiscono appunto al Sole Medio.
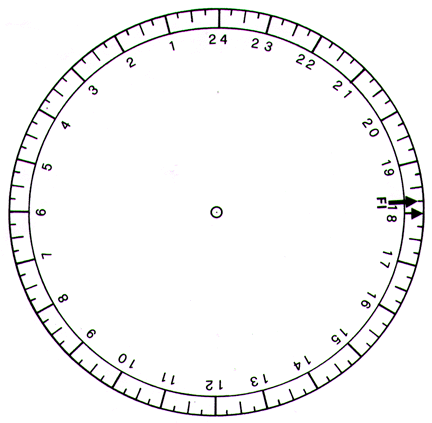
In figura è riportata la posizione della nostra lancetta alle ore 21 del quindicesimo giorno di ogni mese dell'anno: la posizione cambia di circa 30° al mese, poco meno di 1° al giorno. Se vogliamo utilizzarla per sapere che ore sono, dovremo disporre di un orologio con il quadrante delle ore mobile, in modo da poterlo ruotare in senso antiorario di circa un grado al giorno a partire da una posizione iniziale in cui, per esempio, le ore 21 del quadrante vengono indicate dalla nostra lancetta.
il disco delle ore
il disco dell'alidada
Stampate su cartoncino colorato il primo ed il terzo e su plastica trasparente (su lucido) il secondo; ritagliateli lungo i loro bordi e montateli nell'ordine, uno sopra l'altro, congiungendoli con un rivetto forato di diametro non inferiore a 1 cm.
Lo strumento è ora pronto per l'uso. Si possono ottenere due risultati: l'ora della notte conoscendo la data oppure la data conoscendo l'ora.
Per realizzare le due misure è necessario individuare il Grande Carro e la stella Polare e rivolgere verso di essa lo strumento, in modo da traguardare la stella attraverso il foro del rivetto, tenendo l'orologio perpendicolare alla direzione che va dal vostro occhio alla stella ed avendo cura che la figura umana, stilizzata sul disco dei mesi, risulti correttamente orientata.
Determinazione dell'ora Dovete prima di tutto ruotare il disco delle ore fino a portare la freccia lunga, contrassegnata con FI, a coincidere con la data del giorno; poi, rivolto lo strumento verso la Polare, ruotate l'alidada fino a che il suo bordo diritto non sia allineato con la congiungente Dubhe-Merak. In corrispondenza della freccia dell'alidada si legge direttamente il tempo, sul disco delle ore. Determinazione della data Rivolgete lo strumento verso la Polare e ruotare l'alidada fino a che il suo bordo diritto non sia allineato con la congiungente Dubhe-Merak. Senza spostare l'alidada ruotare il disco delle ore fino a che il tempo corrente, segnato dal vostro orologio, sia indicato dalla freccia dell'alidada. La data è indicata dalla freccia lunga contrassegnata con FI del disco delle ore su quello dei mesi. Lo strumento può essere utilizzato in qualsiasi luogo dell'emisfero boreale nel quale il Carro sia sempre visibile su l'orizzonte, tuttavia la sua precisione è massima per i luoghi che si trovano a 3° o 4° ad Ovest del meridiano centrale del proprio fuso orario. Questa è appunto la situazione di Firenze. Possiamo adattarlo alla longitudine di altri luoghi semplicemente spostando la freccia sul disco delle ore. Avete tutti gli elementi per fare da voi questa operazione, tenendo anche conto che l'altra freccia sul disco delle ore è posizionata per i luoghi che si trovano lungo il meridiano centrale.
APPROFONDIMENTO Ho sviluppato la teoria su cui poggia l'orologio notturno in termini del tutto qualitativi, voglio ora mostrare la relazione quantitativa che lega insieme la posizione della lancetta, l'ora e la data. Le due stelle Dubhe e Merak sono effettivamente allineate con la Polare. La loro ascensione retta risulta rispettivamente:
Dubhe alpha UMA 11h:03m:44s Merak beta UMA 11h:01m:51s
Data la piccola differenza le possiamo considerare giacere sullo stesso meridiano celeste per cui, in ogni istante, il loro angolo orario è uguale e questa grandezza definisce la posizione della lancetta. La somma dell'angolo orario AO e della ascensione retta RA di qualsiasi oggetto celeste uguaglia il Tempo Siderale Locale TSL:
TSL = AO + RA Da questa relazione possiamo ricavare l'angolo orario delle due stelle conoscendo il Tempo Siderale Locale. TSL si ottiene dal Tempo Siderale di Greenwich (TSG) semplicemente aggiungendo, con il suo segno, la longitudine del luogo. Per convenzione la longitudine è positiva ad Est di Greenwich, negativa ad Ovest.
TSL = TSG + LONG TSG, infine, si ottiene a partire dal suo valore del primo giorno dell'anno alle ore 00:00 a Greenwich, TSG0h. Esprimendo TSG in ore abbiamo la seguente relazione:
TSG = TSG0h + 0.065709842 * d + 1.00273791 * TU dove
d è il numero progressivo indicante il giorno dell'anno, TU è il Tempo Civile a Greenwich, cioè il tempo trascorso dalla mezzanotte, la costante 1.00273791 è il rapporto tra il numero di ore siderali ed il numero di ore solari medie contenute in un eguale intervallo di tempo e permette quindi la trasformazione del tempo solare in tempo siderale, la costante 0.065709842 esprime in ore siderali la differenza tra un giorno siderale ed un giorno solare medio che è di circa 4 minuti: 0.065709842 ore = 3m 56.556s Possiamo esprimere TU in funzione del Tempo Civile TC di un Fuso Orario n (per convenzione n ha lo stesso segno della longitudine):
TU=TC-n Ed infine otteniamo:
TSL=TSG0h + k1 * d + k2 * (TC-n) + LONG Siamo ora in grado di esprimere la posizione della lancetta in funzione della data d e del tempo civile TC:
AODubhe=TSG0h + k1 * d + k2 * (TC-n) + LONG - ARDubhe Su questa formula si basa l'orologio notturno ed in particolare le sue scale lineari; vi è infatti una relazione di proporzionalità diretta tra la posizione della lancetta, la data ed il tempo civile. Sviluppando il prodotto nel secondo termine abbiamo:
AODubhe = TSG0h + k1 * d + k2 * TC-K2 * n+ LONG - ARDubhe la quantità K2 * n + LONG è la differenza in longitudine tra il luogo ed il meridiano centrale del corrispondente fuso orario. Resta quindi dimostrato che la posizione della lancetta è la stessa in tutti i luoghi aventi la stessa distanza in longitudine dal meridiano centrale.
TSG0h non è costante da un anno all'altro:
1990 TSG0h = 6.626 1991 TSG0h= 6.610 1992 TSG0h = 6.594 1993 TSG0h = 6.644 1994 TSG0h = 6.628 solo gli anni in fase con l'anno bisestile hanno all'incirca lo stesso valore, lo strumento è costruito per il secondo anno successivo a quello bisestile (il 1994, il 1998 per esempio) per cui negli altri anni si commette un errore massimo di due minuti. Questo errore è del tutto trascurabile perchè inferiore alla risoluzione di lettura delle scale ed alla inaccuratezza derivante dalla non concentricità dei dischi. Anche per anni in fase con quello bisestile TSG0h non riassume esattamente lo stesso valore; ciò è dovuto al fatto che l'anno del nostro attuale calendario è leggermente più lungo dell' anno tropico il che produce lo sfasamento di un giorno, tra calendario e stagioni in circa 4000 anni {la durata dell'anno tropico è di 365.2422 giorni solari medi e quella dell'anno del calendario 365.2425}. L'errore che ne deriva fa sentire i suoi effetti sullo zero delle scale in qualche migliaio di anni, quando questo orologio notturno non sarà più utilizzabile poichè la polare non sarà più nella direzione dell'asse terrestre a causa della precessione.
- Questo scritto è stato tratto dal manuale che accompagna il Notturlabio del Comitato per la divulgazione dell'Astronomia, realizzato da Piero Ranfagni.
[Per tornare alla pagina precedente usare il bottone back del browser]
Novembre
Novembre: il bosco fornisce l'ultima raccolta dell'anno, le ghiande preziose per l'ingrasso del maiale.
[Per tornare alla pagina precedente usare il bottone back del browser]
Scale non rotazionali
Una volta constatata la non uniformità di qualunque scala basata sulla rotazione terreste, nel 1956 l'Unione Astronomica Internazionale propose una nuova scala temporale che prese il nome di Tempo delle effemeridi (TE). L'intervallo di scala, il secondo delle effemeridi fu fissato, una volta per tutte, nella 31.556.925,9747-esima parte del tempo che fu necessario al Sole per passare dalla posizione che occupava alle ore 12:00 del 31 Dicembre 1899 alla stessa posizione l'anno dopo (anno tropico 1900). Questo significa che, dalla durata dell'anno 1900, si determinarono le costanti che intervengono nel calcolo del moto dei pianeti, inclusa la Terra e la Luna, e si ricava poi il tempo trascorso dal 1 Gennaio 1900, confrontando le posizioni assunte da questi astri, con quelle previste dalla teoria. Il tempo delle effemeridi, così definito, è una scala uniforme per definizione, in quanto è la variabile indipendente delle equazioni di moto dei pianeti e della luna. In linea di principio quindi, una determinazione del tempo delle effemeridi comporta un'osservazione delle posizioni del Sole e dela Luna. Le posizioni trovate andranno poi confrontate con quelle contenute in una tabella (effemeride), già calcolata, in cui le posizioni sono riportate in funzione del tempo (uniforme) delle effemeridi. Il valore di tempo per cui le posizioni calcolate e quelle osservate conicidono, è il tempo delle effemeridi cercato. Le misure che si debbono fare per determinare le posizioni della Luna e dei pianeti non sono molto precise ed, inoltre, il tempo lo si ottiene solo dopo complesse riduzioni dei dati raccolti. Il risultato finale di questo procedimento, che non è così banale come lo abbiamo descritto, dipende, in maniera sostanziale, dalle equazioni di moto e dalle tecniche di calcolo adotate per ottenere le effemeridi dei diversi corpi del sistema solare. Equazioni e metodi divengono molto complessi quando si cerca di tener conto delle reciproche perturbazioni gravitazionali. Per tutti questi motivi il tempo delle effemeridi non viene più usato come unità di misura, nemmeno per compilare le effemeridi astronomiche, nelle quali, dal 1984, è stato adottato il tempo dinamico terrestre che è un tempo atomico. Data la natura estremamente teorica ed elusiva del tempo delle effemeridi, viene da chiedersi che cosa aveva concretamente in mano l'utente finale, il geodeta ed il navigante, nel breve periodo (1956-1967) in cui questa scala è rimasta in vigore. L'utente disponeva sostanzialmente di un piccolo numero: la differenza tra tempo delle effemeridi e tempo universale in secondi, caratteristica per un determinato anno.
In questo modo disponeva delle posizione dei pianeti, del Sole e della Luna precise, perchè basate su una scala di tempo sicuramente uniforme, e di un valore per calcolare gli angoli orari degli astri, che dipendono dall'effettiva rotazione (non uniforme) della Terra.
Altre informazioni su questi argomenti in rete nei seguenti siti:
Time Service Department U.S. Naval Observatory, Washington, DC NEOSThe National Earth Orientation Service (NEOS)
[Per tornare alla pagina precedente usare il bottone back del browser]
Torna alla pagina principale del Cielo dei Navigatori