Il cielo dei navigatori - Note 5
Da Commissione Divulgazione - Unione Astrofili Italiani.
Indice |
Proiezioni per sviluppo
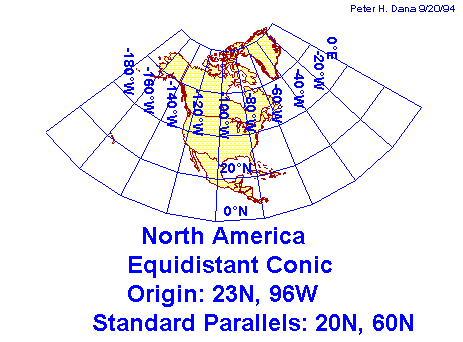
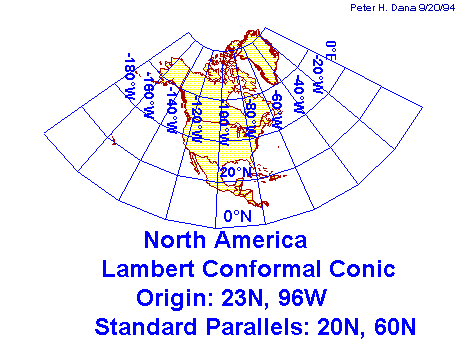
Le proiezioni coniche sono molto utilizzate per rappresentare le medie latitudini. La proiezione conica semplice, sia tangente che secante non conserva alcuna proprietà, per cui nella pratica cartografica, si usano proiezioni coniche modificate e generalmente secanti, in modo da rendere più vasta la superficie con poche e trascurabili distorsioni. Le tre carte seguenti sono proiezioni coniche secanti lungo i paralleli di latitudine 20° e 60° (i paralleli standard), ma differiscono per la proprietà che si è voluto conservare.
La proprietà conservata è l'equivalenza
La proprietà conservata è l'equidistanza
La proprietà conservata è la conformità Le tre carte sembrano uguali, ma non lo sono, lo si vedrebbe bene se si tentasse di sovrapporle. Lo si nota bene confrontando le zone piu' periferiche come la Groenlandia.
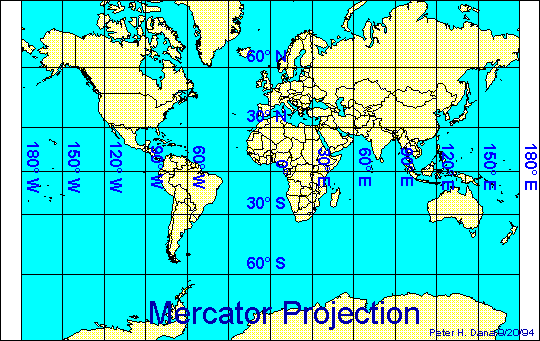
Nella proiezione cilindrica equatoriale semplice, detta del Mercatore, il piano è tangente alla sfera lungo l'equatore pertanto, in questa proiezione, vengono ben rappresentate (con poche distorsioni) le regioni equatoriali, mentre vengono molto distorte le regioni ad alta latitudine. In questa proiezione, però, le linee di rotta (lossodromiche) sono rettilinee, il che la rende utile per la navigazione.
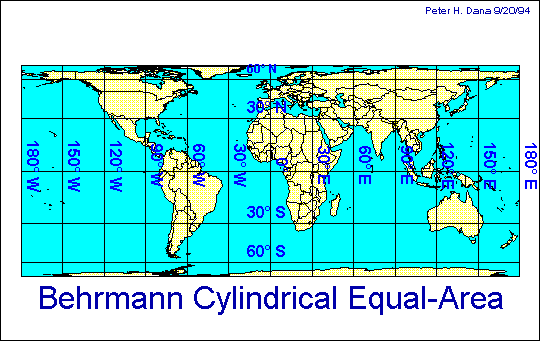
Quando si vogliono conservare altre proprietà, anche le proiezioni cilindriche devono essere modificate. In quella di Behrmann viene conservata l'equivalenza delle superfici. Per far questo l'espansione delle aree in longitudine viene compensata dalla compressione in latitudine: ne consegue che la forma delle terre non viene mantenuta e che la proiezione non è conforme.
[Per tornare alla pagina precedente usare il bottone back del browser]
La Tangente trigonometrica
Si consideri un triangolo rettangolo con vertici A,B,C. Si definisce Tangente trigonometrica dell'angolo di vertice A il rapporto tra il cateto BC ed il cateto AC.
La tabella seguente riporta il valore della tangente trigonometrica, moltiplicata per 100, per alcuni valori dell'angolo compresi tra 0° e 45°. (Si noti che all'angolo di 20° corrisponde il valore della tangente prossimo a quello che dovrebbe aver letto Colombo nell'ambito di una sua misura della latitudine).
angolo in gradi Tangente X 100
0 0
5 9
10 18
15 27
20 36
25 47
30 58
35 70
40 84
45 100
[Per tornare alla pagina precedente usare il bottone back del browser]
Sul valore della sterlina nel 1750
Per avere un'idea del potere d'acquisto della sterlina, alla fine del XVIII secolo, e quindi dell'importanza del premio di 20.000 sterline, messo in palio dal Board of Longitudes, possiamo riferirci a notizie di cronaca del tempo.
Nel 1763 Jerome de Laland scrive che in Inghilterra esistevano cinquanta esattori delle tasse pagati, ciascuno, 250 sterline l'anno. Gli ufficiali giudiziari erano pagati 50 sterline all'anno. Una domestica veniva pagata 47 sterline all'anno Un ricco diplomatico francese che viveva a Londra, arrivava a spendere fino a 850 sterline al mese, metà per i servi e metà per l'affitto della casa.
[Per tornare alla pagina precedente usare il bottone back del browser]
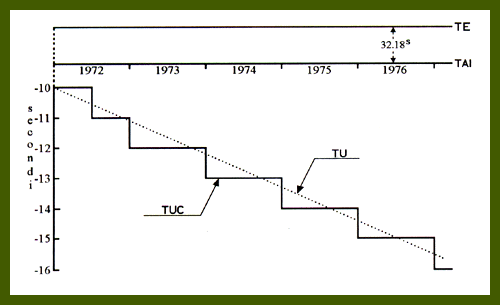
Le scale di tempo atomico
Nel 1967, data la superiore precisione e la grande stabilità raggiunta dagli orologi atomici, è stata introdotta una nuova scala: il Tempo atomico internazionale (TAI). Benchè si tratti di una scala fisica, la sua definizione è in parte astronomica, per avere continuità con le scale precedenti. L'origine è stata fissata alle ore 0 del 1/1/1958 e l'unità di scala è il secondo delle effemeridi, corrispondente alla durata di 9.192.631.770 periodi della radiazione assorbita dall'atomo di cesio 133, nella transizione tra i due livelli iperfini dello stato fondamentale. Può sembrare una definizione astrusa, in realtà si tratta di una definizione operativa a cui corrisponde un'apparechiatura perfettamente stabile e riproducibile. E prorio in questo stà la superiorità dell'orologio atomico rispetto al laborioso calcolo ed all'incosistenza metodologica del tempo delle effemeridi (TE). Dalla definizione di tempo atomico e di tempo delle effemeridi e dal ritardo accumolato dall'orologio terrestre dal 1900 al 1957, discende: TE = TAI + 32,184 sec Se due orologi, uno battente il secondo delle effemeridi e l'altro sincronizzato con il moto di rotazione della Terra, segnavano la stessa ora a mezzogiorno del 31/12/1899, la loro differenza è di 32,184 secondi alle ore 0 dell'1/1/1958. La scala atomica è uniforme, nei limiti delle misure permesse dalla tecnica attuale, e nell'ipotesi, suffragata anche da osservazioni astronomiche, che siano costanti la massa e la carica dell'elettrone, la costante di Planck e la velocità della luce.
Il tempo atomico è trasmesso ed utilizzato come Tempo Universale Coordinato (TUC). Si tratta di una scala ibrida e discontinua la cui origine è fissata alle ore 24 di Tempo Universale del 31/12/71 e l'unità di scala coincide con il secondo delle effemeridi. Una o due volte all'anno, il 31 Luglio e il 31 Dicembre se necessario, viene saltato un secondo (leap second) in modo che la differenza TUC - TU rimanga inferiore a 0.9 secondi. Così, con la stessa scala, si assicura ai fisici un campione rigorosamente costante ed immediatamente disponibile di frequenza e di tempo, ed agli astronomi, ai geodeti ed ai naviganti un tempo strettamente connesso all'orientamento della Terra nello spazio.
Mentre vengono scritti i testi di questo CD-ROM, il servizio del tempo dell'US Naval Observatory ha annunciato la necessità di saltare un altro secondo alla fine del secondo semestre del 1998. Questo porterà la differenza TAI - TUC a 32 sec. a partire dal 1/1/1999.
Altre informazioni, in rete, su questi argomenti nei seguenti siti:
Leap seconds
[Per tornare alla pagina precedente usare il bottone back del browser]
Johann Werner
Johann Werner nacque a Norimberga il 14 Febbraio 1468 e morì, sempre a Norimberga, nel Maggio 1522. Studiò ad Ingolstadt e poi si spostò a Roma, dove venne ordinato prete.
Ritratto di Johann Werner in un'incisione degli inizi del XVII secolo Nel 1503 fu nominato parroco di una piccola chiesa fuori Norimberga, ma poco dopo gli venne affidata la Chiesa di San Giovanni. Werner, nel 1514, pubblicò un insieme di lavori a carattere matematico, astronomico e geografico e, discutendo del metodo delle eclissi di Luna per valutare le longitudine, suggerì di utilizzare anche la posizione della Luna tra le stelle, o la distanza della Luna dal Sole, come "segnale orario" per conoscere il tempo del luogo di riferimento del sistema di longitudini. Nel volgere di qualche anno questa proposta venne ripresa da Pietro Apiano e Gemma Friso. Werner suggeriva di utilizzare la balestriglia, uno strumento non molto preciso per determinare la posizione della Luna, ma ben noto ai naviganti del tempo per misurare l'altezza della stella polare e quindi la latitudine.
Una balestriglia (Museo di Storia della Scienza a Firenze) Scrive Werner:
Sia il nostro scopo quello di trovare la distanza in longitudine tra due luoghi distanti. Il geografo si recherà in uno di questi luoghi e misurerà con la balestriglia la distanza della Luna da una stella dell'Eclittica. Se poi dividiamo questa distanza per il moto della Luna in un'ora sapremo quando la Luna sarà in congiunzione con questo corpo, e quando ancora in futuro.
Il metodo suggerito da Werner non è per niente originale. Un metodo del genere era già stato utilizzato da Amerigo Vespucci che riferiva la posizione della Luna non alle stelle ma al pianeta Marte. Inoltre la teoria del moto della Luna era molto rudimentale e non era possibile preparare effemeridi sufficientemente precise, pertanto il metodo suggerito da Werner era per lo meno prematuro.
[Per tornare alla pagina precedente usare il bottone back del browser]