Il cielo dei navigatori - Introduzione
Da Commissione Divulgazione - Unione Astrofili Italiani.
ATTENZIONE ! - PAGINA IN CORSO DI COMPLETAMENTO !!!
SI DECLINA OGNI RESPONSABILITA' IN MERITO ALLE INFORMAZIONI TRATTE DALLA PRESENTE IN QUANTO NON ANCORA CONTROLLATE E RILASCIATE
Incontriamoci
Incontriamoci: è semplice a dirsi, ma può risultare difficile a farsi. Se uno ci dice incontriamoci e basta è molto probabile che non ci si trovi mai. Perché? Ma è chiaro, non abbiamo detto dove e quando. Ma "dove" ha senso solo se conosciamo il luogo dove ci dobbiamo incontrare e se è ben caratterizzato e circoscritto; provate a prendere un appuntamento in una città, anche piccola, che non conoscete, avrete difficoltà a trovarvi. E anche per il "quando" è lo stesso problema, se non sappiamo riconoscere il momento per il quale è fissato l'appuntamento è probabile che si aspetti a lungo e, forse, inutilmente.
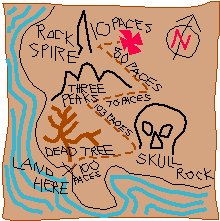
In alcuni casi particolari ce la possiamo fare: possiamo incontrarci, per esempio, davanti alla chiesa principale di una città e al tramonto. In questo caso si dovrà domandare a qualcuno dove si trova la chiesa principale e dovremo guardare il Sole, aspettando che tramonti. Se ci incontriamo in una zona disabitata bisognerà descrivere bene il luogo dell'appuntamento e che questo sia ben riconoscibile; nessuna descrizione risulterà di qualche utilità se ci troviamo in mezzo al mare, nella foresta equatoriale od in un deserto sabbioso o roccioso. E se volessimo incontrarci in un momento della giornata diverso dal tramonto, come riconoscerlo? Potremmo convenire di incontrarci nella prima parte del giorno, durante la mattina, quando ancora il Sole sta salendo nel suo cammino diurno, oppure nel pomeriggio, quando il Sole ha iniziato a scendere. In ogni caso non sapremo mai determinare con precisione il momento e la cosa migliore sarebbe di presentarsi con un certo anticipo, ma quanto tempo sprecato!
Incontrarsi non è facile a meno di non avere una carta dei luoghi (carta topografica) e un orologio. Ambedue sono delle invenzioni abbastanza recenti e se venite con noi andremo a scoprire come gli uomini hanno imparato a conoscere la loro posizione, in terra e in mare, guardando le stelle e rendendosi conto che per definire il quando, ma anche il dove, era indispensabile l'orologio.
I nomi dei luoghi
I luoghi hanno un nome: Firenze, Roma, Parigi, Londra, ma anche più semplicemente l'Impruneta, l'EUR, S.Siro ecc. Ogni volta che si pensa al nome di un luogo ci viene in mente dove è, cioè si pensa al suo posto negli altri e tra gli altri luoghi: Roma è in Italia, Londra in Inghilterra, Parigi è in Francia ed è tra Roma e Londra. Insomma i luoghi hanno un posto, ognuno diverso dall'altro.
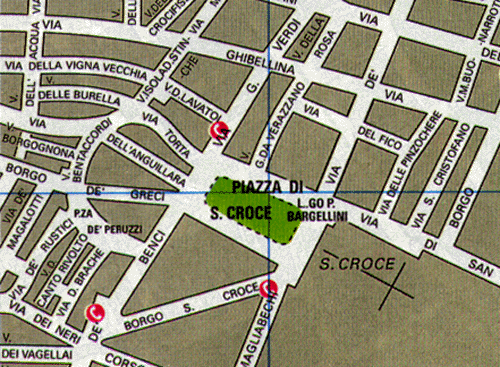
Talvolta il nome rappresenta una vera e propria descrizione delle caratteristiche del luogo cui si riferisce. Ma non sempre è facile riconoscere questa descrizione o servirsene per individuare il luogo, a causa dei cambiamenti linguistici, morfologici ecc. intervenuti nel tempo. Per esempio a Firenze una strada cittadina si chiama "Via Torta" ed in effetti ancora oggi essa corre tutt'intorno ad un isolato, sorto su i resti di un antico anfiteatro romano.
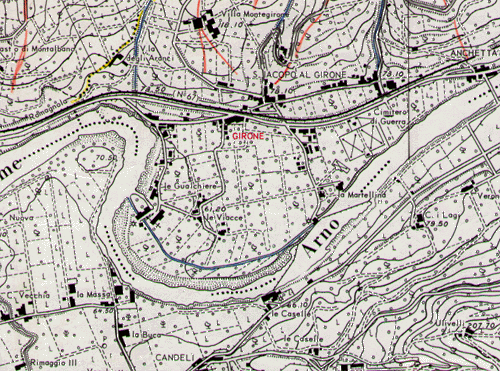
Ad Est di Firenze una piccola frazione si chiama "Il Girone". Qui il corso del fiume Arno è tortuoso perchè, nel terreno pianeggiante, si è formato anticamente un meandro.
Dietro il nome dei luoghi si cela spesso una grande ricchezza culturale: storia, geografia, costume ecc. Ma se dovessimo utilizzare il nome dei luoghi ed il loro significato per riconoscerli, come facevano un tempo contadini, pastori, cacciatori, la nostra mobilità sarebbe molto limitata: impieghremmo dei giorni per spostamenti anche di sole poche decine di chilometri !
I posti dei luoghi
Ogni luogo ha un posto tra gli altri luoghi, ma come fare a comunicare il posto di un luogo? Ecco che nasce spontanea l'esigenza di disegnare su un foglio di carta il posto di un luogo tra gli altri luoghi, per spiegare al nostro interlocutore come fare ad arrivarci. In breve quel foglio di carta diventa la carta o la mappa che indica il posto del luogo. La storia della Geografia è la storia di come l'Uomo ha imparato a fare le mappe per descrivere i posti dei luoghi. Non a caso la parola Geografia, in greco, significa la scienza del disegno della Terra.
È molto importante, nella preparazione di una carta, che si conservino le proporzioni delle distanze tra luogo e luogo. Se non si obbedisce a questa semplice regola, il viaggiatore non potrà pianificare correttamente i tempi di percorrenza del suo viaggio. Siccome però la carta è molto più piccola rispetto alle distanze che intercorrono tra i luoghi che vuole rappresentare, si dovranno ridurre le distanze di un fattore di scala, semplicemente chiamato: scala. Ovvero si dovrà decidere a quale distanza nella realtà, corrisponde un centimetro sulla carta. Se si vuole rappresentare una regione molto grande, molti chilometri corrisponderanno ad un centimetro, se invece si vuole rappresentare una regione piccola, saranno pochi i chilometri che corrispondono ad un centimetro.
Rispetto alla scala le carte si dividono in:
- Planisferi: un centimetro corriponde a 1000 chilometri o più
- Carte Generali: un centimetro corrisponde a distanze comprese tra 1000 e 10 chilometri
- Carte Corografiche: un centimetro corrisponde a distanze comprese tra 10 e 1,5 chilometri
Via via che diminuisce il rapporto di scala, nelle carte si può rappresentare un numero sempre più grande di particolari: abitati, fiumi, torrenti, laghi, strade e ferrovie e, addirittura, il tipo di vegetazione dei boschi e dei campi rappresentati nelle carte topografiche.
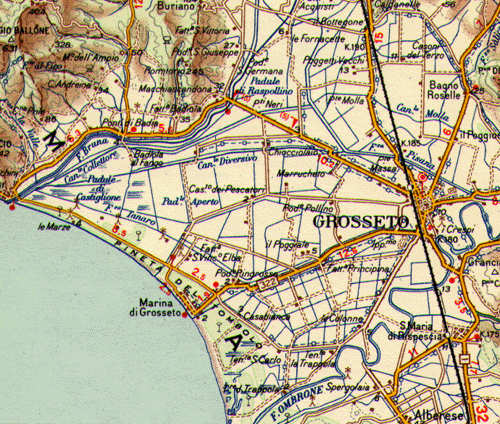
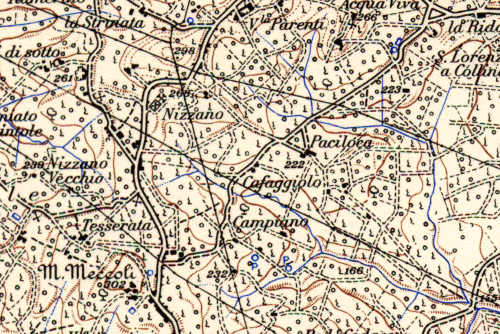
- Nelle carte Topografiche un centimetro va da 1,5 chilometri a 100 metri. In Italia sono molto diffuse le "tavolette" dell'Istituto Geografico Militare (I.G.M.) la cui scala è 1:25.000, un centimetro corrisponde a 250 metri.
Un centimetro corrisponde a 100 metri. La carta è centrata nella località "Cafaggiolo".
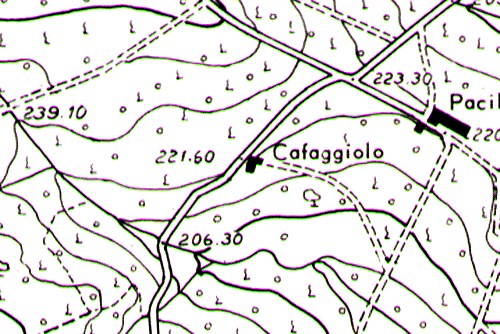
- Nelle Piante o Mappe un centimetro corrisponde a meno di 100 metri.
Un centimetro corrisponde a 50 metri. La carta è centrata nella località "Cafaggiolo".
I posti sulla Terra sono individuati dalle loro coordinate geografiche: una rete di riferimento che consente di determinare il posto di ogni luogo, mediante la sua latitudine e la sua longitudine.
La Terra è una sfera anche se non sembra
La Terra è un Pianeta e, come gli altri pianeti, è un corpo di forma sferica, isolato nello spazio. Queste affermazioni non scaturiscono direttamente dall'esperienza quotidiana, in quanto normalmente viviamo sulla superficie del pianeta che, per le sue dimensioni, ci appare piatta. Oggi, però, abbiamo a disposizione immagini dallo spazio che fanno ormai parte della vita di tutti i giorni: documentari televisivi, servizi meteorologici; queste immagini, meglio di qualunque argomentazione, dimostrano che la Terra è un pianeta.
L'uomo ha intuito e dimostrato la sfericità della Terra anche prima dell'era spaziale, basandosi su diverse esperienze, alcune delle quali, le più semplici, sono qui elencate, proprio perchè chiunque possa ripeterle, senza nessuna particolare attrezzatura ed apprezzando fino in fondo il lungo cammino della Scienza.
1. Se dalla riva del mare vediamo avvicinarsi una nave, ci accorgiamo che per primi compaiono gli alberi, le ciminiere e le parti più alte del ponte e poi, ultimo, lo scafo. Il contrario si verifica se la nave si allontana. Tutto questo non avverrebbe se la Terra fosse piatta.
2. Per un osservatore che si arrampica lungo i fianchi di una montagna l'orizzonte, pur rimanendo circolare, s'ingrandisce via via che aumenta la quota. Tra le infinite figure geometriche solo la sfera ha la proprietà di apparire circolare, da qualsiasi punto la si osservi. 3. Nello stesso istante il cielo diurno o notturno appare diverso ad osservatori posti in luoghi diversi della Terra. In particolare, se ci muoviamo verso Sud, le stelle meridionali ci appaiono via via più alte e sempre più basse quelle settentrionali. Viceversa se ci muoviamo verso Nord. Se due osservatori, in luoghi a diversa longitudine, osservano contemporaneamente il cielo, quello che si trova ad Est vede le stesse stelle in posizione più occidentale dell'altro e viceversa per l'osservatore che si trova più ad Ovest.
4. Durante le eclissi di Luna l'ombra della Terra, proiettata sul nostro satellite, è circolare. Solo un corpo sferico, comunque illuminato, può proiettare un'ombra sempre circolare.
5. Anche usando un piccolo telescopio gli altri corpi del sistema solare ci appaiono di forma sferica ed isolati nello spazio. Per analogia questo dovrebbe valere anche per la Terra.
Le dimensioni della Terra
La Terra non è esattamente sferica, infatti:
- Il diametro equatoriale è leggermente superiore a quello polare.
- La sua superficie presenta valli e montagne, punti più alti e punti più bassi rispetto a qualsiasi livello medio.
Possiamo quindi definire la Terra un ellissoide di rotazione (una specie di pallone da rugby) rugoso. Non dimentichiamo però che schiacciamento e rugosità sono del tutto trascurabili rispetto alle sue dimensioni, ed è per questo che, dallo spazio, ci appare perfettamente sferica. Lo possiamo constatare dalle seguenti misure:
| Raggio Equatoriale (R) | Km. 6.378,4 |
| Raggio Polare (R') | Km. 6.356,9 |
| Differenza (R - R') | Km. 21.5 |
| Schiacciamento ([R - R']/R) | |
| Circonferenza equatoriale | Km. 40.076,6 |
| Lunghezza del Meridiano | Km. 40.008,9 |
| Superficie | Km2. 509.950,414 |
| Volume | Km3. 1.083.000.000 |
| Monte Everest | m. 8.882 |
| Fossa di Emden | m. -10.793 |
(L'immagine dell'eclissi di Luna ci è stata data dall' Osservatorio Torre Luciana.)
Le proiezioni cartografiche
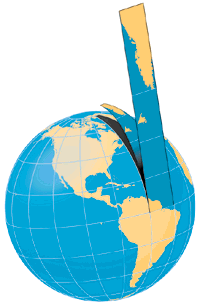
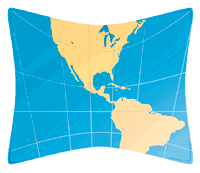
Il problema che deve affrontare chi disegna le carte geografiche consiste nel trovare un accorgimento per rappresentare una superficie sferica (la Terra) su un foglio piano (la carta geografica). Il problema non si pone quando si vogliono rappresentare piccolissime porzioni di superficie terrestre (per esempio le carte catastali), ma diventa notevole quando le aree da rappresentare sono molto grandi. Si parla allora di proiezioni cartografiche, cioè di un insieme di regole che permettono di riportare sul piano della carta ogni punto della superficie terrestre rappresentata. Non è possibile spianare una superficie sferica o, più in generale curva, senza deformarla, cioè senza apportare compressioni ed espansioni ad alcune, se non a tutte le sue parti.
| Non è possibile spianare una superficie sferica o, più in generale curva, senza deformarla, cioè senza apportare compressioni ed espansioni ad alcune, se non a tutte le sue parti.
| 
|
Si può però scegliere quali distorsioni introdurre e quali proprietà conservare.
|
|
|
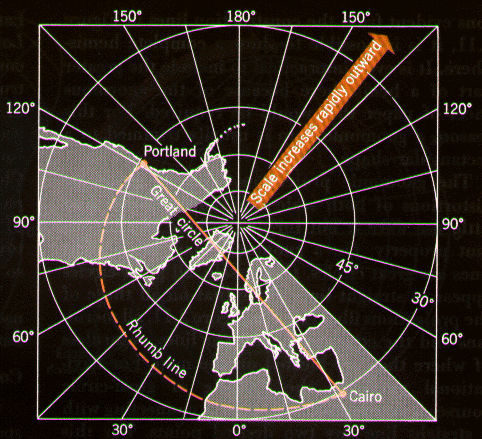
Un'altra interessante proprietà, molto utile nella navigazione, è data dalla rappresentazione delle linee ortodromica e lossodromica:
- la linea lossodromica o linea di rotta o Rhumb line è la linea che unisce due punti sulla carta, formando lo stesso angolo con tutti i meridiani e paralleli intersecati.
- la linea ortodromica o arco di grande circolo è la più breve congiungente tra due punti sulla Terra.
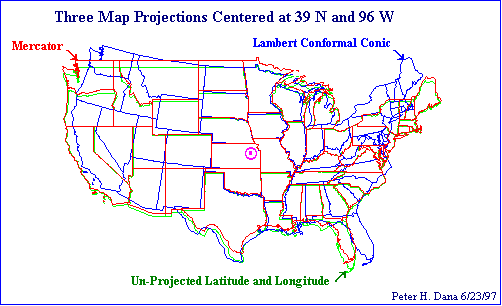
Dobbiamo la gran parte delle immagini usate in questa pagina a Peter H. Dana, docente presso il Department of Geography, University of Texas at Austin che è autore di interessanti lezioni sull'argomento.
La geometria delle proiezioni cartografiche
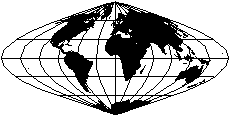
Ci sono diversi metodi per realizzare le carte geografiche. Si sceglie l'uno o l'altro a seconda della localizzazione sulla Terra della superficie terrestre che si vuol rappresentare e delle proprietà che si vogliono conservare. Tutti i metodi, comunque, derivano da un'operazione geometrica detta proiezione. Una sfera (o una porzione di essa) può essere proiettata su un piano in due soli modi, il che ci permette così di classificare le proiezioni in:
Nelle proiezioni prospettiche il piano di proiezione può essere tangente o secante ed in quest'ultimo caso passare o no per il centro della sfera.
Lungo la retta pependicolare al piano di proiezione e passante per il centro della sfera viene fissato il punto di vista. Da esso si tracciano le congiungenti con i punti della Terra che si vogliono rappresentare; le loro intersezioni con il piano costituiscono la carta geografica. La posizione del punto di vista permette di costruire differenti proiezioni azimutali.
Nelle proiezioni per sviluppo la Terra viene avvolta da una superficie conica o cilindrica che può essere tangente o secante e viene scelto un opportuno punto di vista che, generalmente, coincide con il centro della sfera. Una volta che i vari punti della Terra sono stati proiettati, la superficie viene svolta e si ottiene la carta geografica piana.
Il cilindro può essere tangente o secare la Terra lungo l'equatore (Proiezioni Normali), lungo un meridiano (Proiezioni Trasverse) o lungo un cerchio qualsiasi (Proiezioni Oblique).
Anche in questo caso la posizione del punto di vista permette di realizzare differenti proiezioni per sviluppo
Dobbiamo la gran parte delle immagini usate in questa pagina ed in quelle ad essa correlate a Peter H. Dana, docente presso il Department of Geography, University of Texas at Austin che è autore di interessanti lezioni sull'argomento.
I cieli dei luoghi e i sistemi di riferimento astronomici
Ogni luogo ha un cielo, luoghi diversi hanno cieli diversi, il cielo di un luogo cambia con il tempo. Cerchiamo di essere più precisi:
- Nello stesso luogo il cielo è diverso ad ore diverse dello stesso giorno. Un esempio
- Nello stesso luogo il cielo è diverso alla stessa ora di giorni diversi. Un esempio
- Nello stesso istante il cielo è diverso, se osservato da luoghi diversi della Terra. Un esempio
Di giorno, il cielo ci appare come una grande sfera di colore azzurro su cui possiamo riconoscere il Sole e talvolta la Luna. Di notte il cielo si popola di stelle, talvolta si vedono i pianeti e la Luna. Come di giorno gli oggetti celesti ci appaiono tutti alla stessa distanza, da qui la sensazione di essere sotto una grande volta appoggiata al cerchio dell'orizzonte: la sfera celeste.
Durante la notte, così come durante il giorno, il cielo pare ruotare da Est verso Ovest e trascinare nel suo apparente movimento tutti i corpi celesti che, al passare del tempo, cambiano posizione rispetto all'orizzonte; alcuni di essi rimangono sempre visibili, altri sorgono e tramontano. Tutto questo è la conseguenza della rotazione della Terra da Ovest verso Est, in senso antiorario.
Le stelle, visibili in una certa direzione alla stessa ora della notte, cambiano durante l'anno. Durante l'anno cambia anche l'altezza del Sole a mezzogiorno e il punto da cui sorge e in cui tramonta. Tutto questo è la conseguenza del moto di rivoluzione della Terra attorno al Sole. Non è sufficiente descrivere qualitativamente il cambiamento del cielo, per potersi orientare in cielo e sulla Terra è necessario descrivere quantitativamente la posizione delle stelle. Esse ci appaiono alla superficie della sfera celeste e, su una sfera, un punto è definito da una coppia di coordinate che misurano la sua distanza angolare da due piani di riferimento; essi prendono il nome di piano fondamentale e piano origine. La scelta dei piani di riferimento è arbitraria e ogni coppia di piani definisce un sistema di coordinate.
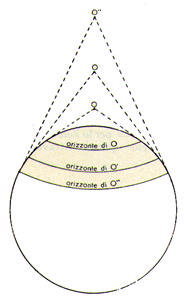
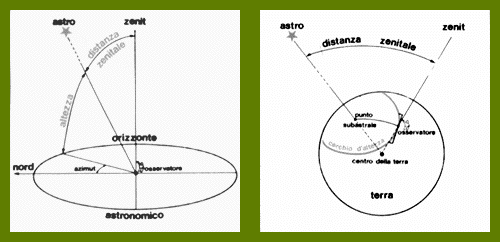
Il modo più semplice per indicare la posizione di un oggetto in cielo è quello di utilizzare il sistema di riferimento detto alto-azimutale, le cui coordinate sono l'azimut e l'altezza. Durante il giorno cambiano continuamente l'altezza e l'azimut del Sole e lo stesso accade, di notte, per le stelle, ma non tutte della stessa quantità. Al passare del tempo, alcune sorgono e tramontano, sono perciò visibili solo per una parte della notte e prendono il nome di stelle occidue. Altre, pur cambiando posizione, si mantengono sempre sopra l'orizzonte e vengono chiamate stelle circumpolari. L'appartenenza di una stella al gruppo delle occidue o delle circumpolari dipende dalla latitudine del luogo di osservazione; all'equatore tutte le stelle sono occidue, ai poli tutte sono circumpolari. La stella circumpolare più lontana dal polo celeste si muove, apparentemente, percorrendo un cerchio tangente all'orizzonte, che gli antichi chiamavano circolo artico. Nell'emisfero settentrionale ed in questo periodo storico, c'è una stella che rimane praticamente ferma, cioè mantiene grosso modo la stessa altezza e lo stesso azimut, a qualunque ora della notte ed in qualunque notte dell'anno: la Polare Questa stella si trova per caso molto vicina (meno di un grado) al Polo Nord Celeste, il punto della sfera celeste verso cui è diretto l'asse di rotazione terrestre.
Per ovviare al problema che pone la continua variazione delle posizioni delle stelle e del Sole durante il giorno e la notte, gli astronomi ricorrono al sistema di riferimento equatoriale relativo. Una paziente osservazione durante tutta la notte od una foto a lunga esposizione, ci mostrano che le stelle si muovono apparentemente lungo traiettorie circolari e parallele, che diventano sempre più piccole quanto più sono vicine all'asse di rotazione della sfera celeste.
Le traiettorie con raggio maggiore individuano il piano dell' Equatore Celeste; la distanza di ciascuna stella rispetto a questo piano è costante, risulta così naturale prendere questo piano come base di un nuovo sistema di riferimento (Sistema Equatoriale) e la distanza costante come una delle sue coordinate: la Declinazione. L'altra coordinata, qualunque sia il suo piano di riferimento, varia continuamente, ma uniformemente con il tempo. La si misura a partire dal meridiano locale verso Ovest in senso orario e prende il nome di Angolo Orario. L'angolo orario di una stella indica così di quanto la Terra ha ruotato dopo il passaggio di quella stella in meridiano, cioè quanto tempo è passato. Per questo motivo l'angolo orario si misura in ore, minuti e secondi; tenendo conto che 24 ore di angolo orario corrispondono ad un'intera rotazione della Terra che riporta così le stelle nella stessa direzione, un'ora corrisponde a 15 gradi, un minuto di tempo a 15 primi ed un secondo di tempo a 15 secondi di grado. Il tempo che deriva dall'angolo orario di un oggetto celeste e quindi dalla rotazione della Terra, prende il nome di Tempo rotazionale per distinguerlo da altri tipi di tempo, basati cioè su altri fenomeni ed altri tipi di misura
Gli astronomi però non si sono accontentati perché il sistema di riferimento equatoriale relativo, anche se più comodo, ha sempre una coordinata che varia nel tempo, quella che appunto abbiamo chiamato angolo orario che, inoltre, risulta diversa per osservatori che non si trovano lungo lo stesso meridiano terrestre. Per avere coordinate celesti che non variano nel tempo e che rimangano costanti per qualsiasi osservatore sulla Terra, è stato introdotto un terzo sistema di riferimento, detto equatoriale assoluto. Questo sistema è quello che si usa per disegnare le posizioni delle stelle sui globi celesti, le carte, gli atlanti celesti oppure per compilare cataloghi di oggetti quali galassie, stelle, nebulose ecc.
Per rappresentare la posizione degli astri in cielo si utilizzano gli stessi sistemi di proiezione che vengono utilizzati per la posizione dei luoghi geografici. In questo modo è possibile disegnare delle carte del cielo nel sistema di riferimento alto azimutale, nel sistema equatoriale relativo, e nel sistema assoluto.
Sole, Stelle e Latitudine
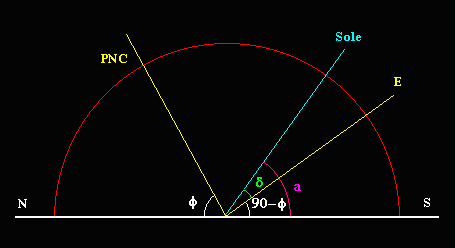
Viene definita latitudine di un luogo l'angolo compreso tra l'equatore celeste (EQ) e lo zenit (Z), che è il punto d'incontro della sfera celaste con la verticale del luogo. Purtoppo in cielo non sono riconoscibili nè l'equatore nè lo zenit e questa definizione non è operativa.
Osserviamo però che quest'angolo è uguale a quello compreso tra l'orizzonte ed il Polo Nord Celeste, poichè sono entrambi complementari dello stesso angolo ZEPNC, compreso tra lo Zenit ed il Polo Nord Celeste. Quest'ultimo è, in prima approssimazione, contrassegnato dalla stella polare e basterà quindi misurare la sua altezza per conoscere la latitudine di un luogo.
A causa della sfericità della Terra, osservatori in luoghi diversi (e quindi con diverse coordinate geografiche) misurano coordinate altoazimutali diverse per lo stesso astro, osservato contemporaneamente.
Se un astro culmina sul meridiano comune di due osservatori alla stessa longitudine, ma a diversa latitudine, di esso viene misurato lo stesso azimut, pari a 180 ° e la differenza delle altezze meridiane è pari, in valore assoluto, alla differenza delle latitudini.
Possiamo così trovare la latitudine di un luogo se conosciamo la latitudine di un altro luogo e se veniamo a sapere l'altezza alla culminazione di un astro in entrambi. Questo metodo non è di grande utilità per un viaggiatore, ma ci indica che, con oggetti in meridiano, la relazione tra latitudine ed altezza è senz'altro semplice.
Consideriamo ora una qualunque stella, Sole compreso, in culminazione meridiana:
L'altezza meridiana dell'astro è uguale alla somma della sua declinazione e dell'inclinazione dell'Equatore sul piano dell'orizzonte. L'Equatore forma con l'orizzonte un angolo pari al complemento della latitudine, per cui:
La declinazione è una coordinata del sistema equatoriale e quindi uguale per tutti gli osservatori. Se si tratta di una stella possiamo considerarla costante nel tempo (almeno in prima approssimazione), se si tratta del Sole, la sua declinazione riassume ogni anno, alla stessa data, lo stesso valore, per cui può essere ricavata da un calendario astronomico, conoscendo la data dell'osservazione.
Non è facile misurare in mare, con la nave in moto, l'altezza meridiana di un astro, perchè la bussola non riesce ad indicare con sufficiente precisione la direzione Nord-Sud, e perchè, non conoscendo esattamente la longitudine, non si conosce il momento esatto della culminazine. Sulla terraferma è invece una misura facile che è stata possibile fin dall'antichità con uno strumento molto semplice: lo Gnomone. Esso consiste in un bastone, un obelisco, una colonna. Si determina, prima di tutto, la direzione Nord-Sud, ossia la linea meridiana.
Al mattino l'ombra dello gnomone è lunga e diviene sempre più corta via via che ci si avvicina alla culminazione, cioè il mezzogiorno solare vero locale. Dopo mezzogiorno, nel pomeriggio, l'ombra torna ad allungarsi, ma nel momento della culminazione la sua lunghezza varia pochissimo, mentre varia velocemente la sua direzione. Insomma non è possibile determinare la direzione Nord-Sud come la direzione dell'ombra più corta, senza commettere grossolani errori. Gli antichi ricorrevano al metodo dei cerchi dell'Indo: poichè ad uguali intervalli di tempo, prima e dopo la culminazione, il Sole ha la stessa altezza sull'orizzonte, ombre uguali dello gnomone individuano la direzione dell'astro in questi istanti e queste direzioni sono simmetriche rispetto alla direzione meridiana. La direzione Nord-Sud resta così determinata dalla direzione della bisettrice dell'angolo formato da due ombre di uguale lunghezza. Quando l'ombra del bastone si proietta lungo la linea meridiana determiniamo, contemporaneamente, l'istante della culminazione e la lunghezza meridiana dell'ombra.
Il rapporto h/l tra l'altezza del bastone e la lunghezza della sua ombra è la tangente trigonometrica dell'angolo che si vuol misurare. Si può ricavare l'ampiezza di quest'angolo senza fare ricorso alla trigonometria: si disegna un triangolo rettangolo con i cateti in scala rispetto alle misure dih edle si misura, con un goniometro, l'angolo compreso che, per la similitudine dei triangoli è perfettamente uguale all'altezza meridiana del Sole.
Il Tempo e la sua misura
C'è nella storia dell'Umanità un insopprimibile bisogno di misurare il tempo e questo bisogno è "senza tempo": nasce con l'uomo e lo accompagna, sempre presente e pur diverso, nell'evoluzione e nell'articolazione delle varie culture. Non è possibile, in questo CD, parlare compiutamente del tempo; ci limiteremo alla sua misura in occidente e solo a quegli aspetti che ci servono per la Geografia e la Navigazione. Approfondite da voi questo argomento, magari partendo dagli indirizzi che vi forniamo alla fine della pagina, e gustatevi le seguenti rappresentazioni dei mesi del calendario che vogliono ricordarvi come, da migliaia di anni, l'uomo cerchi di allineare il calendario civile con quello astronomico. Le immagini provengono dal manoscritto "Trés Riches Heures conservato nel museo di Chantilly e furono realizzate tra il 1412 ed il 1416 da i fratelli Limbourg, Paul, Hermann e Jean. Se osservate attentamente, nell'epoca in cui le immagini furono dipinte, le stagioni non iniziavano nelle stesse date di oggi. Sapete dire perchè?
| Gennaio | Febbraio | Marzo | Aprile | Maggio | Giugno |
| Luglio | Agosto | Settembre | Ottobre | Novembre | Dicembre |
Un po' di teoria: Qualunque sia il metodo o lo strumento usati, la misura del tempo consiste nel collocare uno o più avvenimenti in una scala ordinata di eventi; otteniamo così la data dell'avvenimento, riferita all'origine della scala, ovvero il tempo trascorso tra due avvenimenti. Non fatevi impressionare da queste definizioni astratte, facciamo subito un esempio: immaginiamo che da una scatola, ad intervalli regolari, fuoriescano delle palle da biliardo. Mentre cade la terza palla inizio a scrivere questa riga di testo e finisco poco dopo che è caduta la quarta. Ebbene la mia azione è databile in "palla tre" e dura poco più dell'intervallo che intercorre tra la caduta di una palla e l'altra. La regolare caduta delle palle è una scala ordinata di eventi.
Una scala ordinata di eventi, o scala temporale, è un'ordinata successione di valori assunti da una qualunque grandezza misurabile, in quanto non misuriamo il tempo, ma le variazioni delle grandezze, assumendo che queste rappresentino il suo fluire. In linea di principio, qualunque fenomeno noto può essere utilizzato. Esistono così diverse scale temporali. La bontà di una scala può essere giudicata in base alle necessità soggettive del singolo utente o in base a caratteristiche oggettive che sono state individuate fin dal XVII secolo. Una scala temporale deve essere perenne, universale, affidabile, precisa ed uniforme. Le scale astronomiche sono indubbiamente perenni, universali ed affidabili, ma poco precise e non sappiamo se intrinsecamente uniformi.
L'astronomia moderna considera l'universo in continua evoluzione, cioè in continua trasformazione nel tempo. Possiamo allora utilizzare qualunque grandezza che lo descrive per costituire una scala temporale: la sua densità, la temperatura, la composizione chimica ecc. Se però vogliamo misure precise, le scale astronomiche concretamente usate derivano tutte da misure di posizione di un corpo celeste. Alcuni dei fenomeni astronomici che sono stati maggiormente usati nel passato per misurare il tempo o che lo sono ancora oggi sono i seguenti:
- L'alternarsi del giorno e della notte
- le fasi della Luna
- il sorgere, tramontare e culminare del Sole, della Luna e delle stelle
- il succedersi delle stagioni
- le eclissi e, in genere, le occultazioni
- le posizioni dei satelliti rispetto al pianeta
- la posizione, relativa alla stelle fisse, del Sole, della Luna e dei pianeti
Il moto apparente o reale dei corpi celesti non è uniforme, nè ci possiamo aspettare che lo sia in un universo dominato dalla gravità e dove non esistono corpi isolati. Ne segue che qualunque scala, corrispondente ad incrementi uguali di una qualunque coordinata spaziale od angolare, risulterà tanto meno uniforme quanto più precise saranno le misure. Con aggiustamenti teorici e considerando la variazione media di una grandezza, generalmente il moto medio, potremo costruire una scala che risulterà tanto più uniforme quanto più completa è la comprensione del fenomeno, cioè quanto più soddisfacente è la teoria usata per descriverlo. Non meravigliamoci allora che, fin dall'antichità, l'Astronomia propose tempi veri e medi e quantità equanti, cioè quantità che bisogna aggiungere a grandezze non uniformi per renderle tali.
Possiamo dividere in due gruppi le scale astronomiche:
- Scale rotazionali. Si basano sui moti apparenti dei corpi celesti, dovuti a quello reale di rotazione della Terra.
- Scale non rotazionali. Si basano sul moto di rivoluzione della Terra e degli altri corpi del sistema solare.
Negli anni 50 e 60 divennero disponibili gli orologi atomici e con essi fu possibile misurare il tempo con una precisione centinaia di migliaia di volte maggiore di quella ottenibile con metodi astronomici. Per migliaia di anni l'astronomo è stato il signore incontrastato del tempo, le sue misure servivano di base per tutte le altre misure di tempo, sia nella vita civile che nella ricerca scientifica, dal 1961 questo ruolo è passato al fisico atomico. Ma ciò non significa che non abbia più senso misurare la posizione dei corpi celesti. Prima di tutto, il tempo basato sulla posizione dei corpi celesti permette ancora oggi di trovare la propria posizione sulla Terra ed, inoltre, dal confronto tra il tempo dedotto dalle osservazioni astronomiche ed il tempo atomico, verranno nuovi dati per la comprensione del moto di rotazione e rivoluzione della Terra, per il miglioramento dei metodi di studio dei moti orbitali, per la determinazione delle componenti non gravitazionali nell'accelerazione dei corpi celesti, per lo studio della costante di gravità ecc....
Tempo, stelle e longitudine
Se la Terra fosse piana invece che sferica, da ogni luogo della Terra si vedrebbe, in ogni momento, lo stesso cielo e tutto il mondo avrebbe la stessa ora. Il Sole sorgerebbe e tramonterebbe per tutti nello stesso istante, come succede in effetti per una limitata estensione di territorio, cioè per una piccola superficie terreste che, proprio perchè piccola, può essere approssimata ad un piano. Ma su grandi estensioni le cose cambiano. Quando il Sole sorge in Italia, in America è ancora notte profonda, invece quando sorge in America in Europa è quasi la metà del giorno. La stesso accade per le stelle. Quando una stella sorge in Europa, in America è ancora sotto l'orizzonte, e quando sorge in America, in Europa è alta nel cielo, ma la stella, nell'universo, è sempre nello stesso posto. Siamo noi, sulla Terra, che stiamo girando intorno all'asse del nostro pianeta alla velocità di un giro ogni ventiquattro ore.
Quando un astro si trova a transitare per il piano verticale, che passa per i punti Nord e Sud dell'orizzonte, si dice che transita al meridiano del luogo. Se allora un astro impiega un certo tempo per passare dal meridiano di un luogo al meridiano di un altro luogo, questo significa che è la Terra ad impiegare quel tempo per ruotare di un angolo pari alla differenza di longitudine tra i due luoghi.
Se quindi, navigando anche in mari lontani, porto con me un orologio regolato sul tempo del meridiano di riferimento (quello di Greenwich da 200 anni a questa parte), e delle tavole che forniscono i tempi di culminazione di certe stelle su questo meridiano, la differenza tra i tempi di culminazione locale e quella delle tavole mi dà proprio la longitudine del luogo.
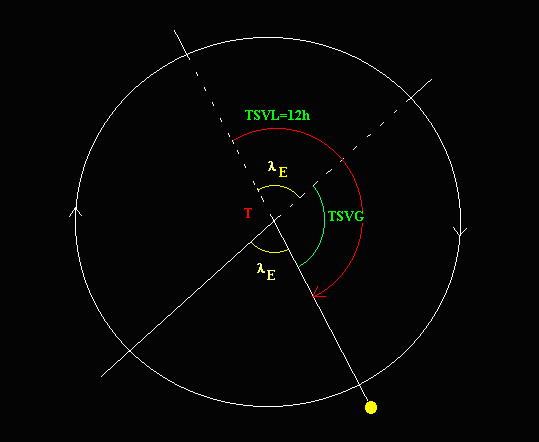
La figura rappresenta la sezione equatoriale della sfera celeste e mostra questo ragionamento per il Sole. Il Tempo Solare Vero Locale (TSVL) è l'angolo orario del Sole aumentato di 12 ore, in quanto misurato a partire dall'antimeridiano locale, cioè dalla mezzanotte. La differenza tra il Tempo Solare Vero Locale e quello misurato lungo il meridiano di riferimento, cioè il Tempo Solare Vero a Greenwich, è la differenza di longitudine tra i due luoghi.
Possiamo fare una misura di longitudine utilizzando lo Gnomone. Quando la sua ombra si proietta lungo la linea meridiana quello è l'istante del mezzogiorno solare vero locale. Indicando con LONG la longitudine del luogo dove culmina il Sole, con E l'equazione del tempo e con TU il tempo universale, ossia il tempo solare medio a Greenwich (TSMG) abbiamo: TSVG = TSVL - LONG
TSVG = TSMG + E = TU + E
TU + E = TSVL - LONG = 12h - LONG
LONG = 12 - TU - E
Per l'Italia TU si ottiene semplicemente sottraendo un'ora dal tempo indicato dall'orologio, due ore se è in vigore l'ora legale. Potete consultare in rete l'annuario dell'Osservatorio astrofisico di Arcetri per ottenere il valore dell'equazione del tempo nei vari giorni dell'anno.
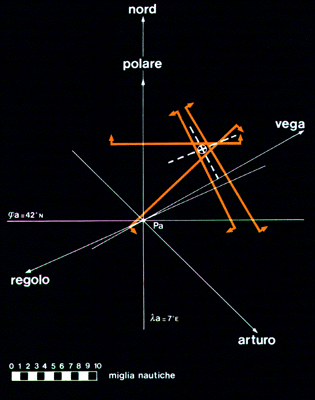
Il Punto nave, ovvero come fanno i marinai
Come trovare la propria posizione in qualsiasi momento
Il viaggiatore desidera conoscere la propria posizione in un qualsiasi momento del giorno o della notte in modo da correggere la rotta e non allungare inutilmente i tempi del suo viaggio. Basarsi quindi su gli astri che si trovano in meridiano per ricavare la latitudine e la longitudine non è un metodo molto efficiente, anche perchè ci potrebbe essere una nuvola, in quella direzione, al momento della misura. Il problema deve potersi risolvere in qualsiasi momento, con qualsiasi astro, in qualunque direzione si trovi. La soluzione del problema è alla base del successo commerciale delle traversate oceaniche del secolo scorso. A causa della sfericità della Terra e dei suoi movimenti, le coordinate alto-azimutali di un astro (stelle, Sole, Luna, pianeti), dipendono da:
- le sue coordinate equatoriali
- le coordinate geografiche dell'osservatore
- il tempo, ossia l'orientamento e la posizione della Terra rispetto alle stelle
Quindi, se conosciamo:
- le coordinate equatoriali dell'astro
- le sue coordinate alto-azimutali in un certo istante
- il tempo
da questi dati è possibile ricavare le coordinate geografiche del luogo, qualunque sia l'astro e qualunque sia la sua posizione rispetto all'orizzonte ed al meridiano di chi lo osserva. L`Astronomia sferica ci fornisce le formule ed i metodi per risolvere questo problema. Praticamente, chi viaggia preferisce non utilizzare misure di azimut in mare, perchè lo impediscono i movimenti di rollio e beccheggio della nave, ed in terra, in quanto generalmente, non si conosce la direzione Nord-Sud, perchè non è immediato ricavarla durante il viaggio. Si preferisce allora misurare la sola altezza di più astri ed il tempo corrispondente, riferito al meridiano terrestre di longitudine zero. La misura di altezza risulta facile e precisa, anche in mare, mediante un ingegnoso strumento, il sestante. La scelta di basare il calcolo della latitudine e longitudine su sole misure di altezza e di tempo determina il particolare metodo cosiddetto dei cerchi di altezza che, assieme al sestante ed al cronometro marino, è il simbolo stesso della navigazione astronomica degli ultimi due secoli.
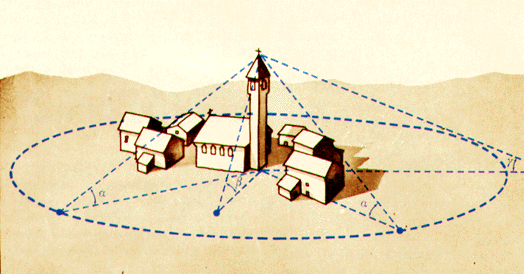
Esistono infiniti punti della Terra dai quali, ad un certo istante, gli osservatori misurano una data altezza dello stesso astro; questi punti sono disposti lungo un cerchio, il cui centro si trova nel luogo che, in quell'istante, ha l'astro allo zenit, e che prende perciò il nome di punto substellare.
Lo si capisce facilmente pensando ad un oggetto terrestre come la punta di un campanile: tutti coloro che misurano la stessa altezza angolare si trovano alla stessa distanza lineare dalla base del campanile e quindi lungo un cerchio. Coloro che misurano un'altezza angolare minore si trovano su un cerchio concentrico con raggio maggiore e, viceversa, minore se misurano un'altezza angolare maggiore. Coloro che misurano un angolo retto si trovano alla base del campanile.
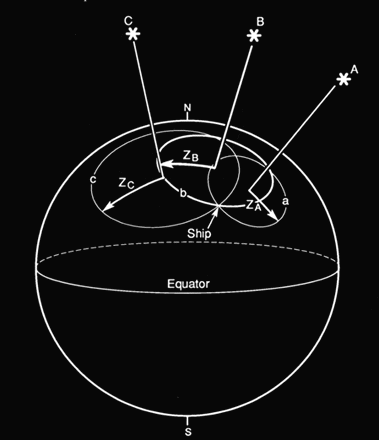
Tutto ciò resta valido anche con le stelle, soltanto che, diversamente che con il campanile, le misure devono essere riferite ad un preciso istante, cioè ad una precisa posizione della Terra rispetto alle stelle, a causa dell'apparente moto di rotazione del cielo. Il raggio del cerchio è pari al complemento dell'altezza misurata. Questa grandezza viene indicata distanza zenitale. Il cerchio, così definito, prende il nome di cerchio di altezza. Con due astri si hanno due cerchi di altezza e l'osservatore DEVE trovarsi in uno dei due punti d'incontro dei due cerchi. Resta quindi un certo margine di ambiguità anche se, normalmente, i due punti cadono molto distanti l'uno dall'altro ed il navigante può facilmente escluderne uno. Se consideriamo tre astri ed i corrispondenti cerchi di altezza, l'osservatore DEVE trovarsi nell'unico punto d'incontro di questi tre cerchi ed il problema è ora perfettamente determinato.
Come trovare le coordinate geografiche di questo punto? Oggi lo possiamo fare con il calcolo, utilizzando una semplice calcolatrice programmabile che, in pochi secondi, risolve il sistema di equazioni che rappresentano la sfera terrestre ed i piani che la intersecano lungo i cerchi di altezza. Questo metodo, senza l'ausilio delle moderne calcolatrici, non era proponibile (e non lo è nemmeno adesso) a bordo di una nave: troppo lungo e complesso. Prima di ottenere il risultato la nave ha tutto il tempo di infrangersi su una scogliera o di arenarsi su un basso fondale !! L'altra soluzione è il metodo grafico, consistente nel disegnare i cerchi di altezza su una rappresentazione cartografica della Terra. Purtroppo i cerchi rimangono tali solo e soltanto su un mappamondo che, per garantire la precisione desiderata, dovrebbe essere grande quanto la nave !! In qualunque altra proiezione cartografica i cerchi diventano curve, molto difficili da disegnare. Ma, qualunque sia la proiezione usata, in una carta che, per essere accurata, rappresenta sempre una superficie limitata, si possono disegnare solo piccolissime porzioni dei cerchi di altezza e non è possibile avere insieme i cerchi ed i loro centri, cioè i punti substellari. Inoltre poichè un piccolo arco di un grande cerchio si confonde con la sua corda, i cerchi compaionio nelle carte come segmenti rettilinei detti rette di altezza.
A causa degli inevitabili errori di misura, dovuti principalmente alla misura dell'altezza, poichè l'orologio è ormai più preciso del sestante, le rette di altezza non si incontrano mai in un punto, come assicura la teoria. Esse delimitano sulla carta un'area dentro la quale viene sicuramente a trovarsi la nave. Tanto maggiore è l'accuratezza della misura, tanto più piccola l'area di incertezza. Con questo metodo, con un pò di esperienza, un buon orologio ed un buon sestante, si può determinare la posizione della nave con lo scarto di non più di due chiliometri. Calcolo e disegno delle rette di altezza viene insegnato nei corsi annuali di navigazione astronomica delle accademie navali e degli istituti nautici; non c'è qui lo spazio per entrare nei dettagli, possiamo però chiarire gli aspetti astronomici del calcolo dei cerchi di altezza, accontentandoci di disegnarli direttamente su un mappamondo nell'ambito di un' esperienza didattica.
Se al posto delle stelle avessimo in cielo oggetti artificiali, sempre visibili anche con le nuvole, il metodo risulterebbe sempre valido e, senzaltro, più vantaggioso. Attualmente viene usata una rete di satelliti artificiali in orbita attorno alla Terra in numero tale che, da ogni luogo, ne sono visibili almeno quattro, sufficienti per calcolare, senza alcuna ambiguità, le coordinate geografiche.
Poichè di ogni satellite si conosce la posizione nello spazio e se ne misura la distanza, l'osservatore si trova alla superficie di un'enorme sfera centrata sul satellite ed avente come raggio quella distanza. La sua posizione sulla Terra risuterà dall'intersezione della sfera terrestre e da quelle di almeno tre di questi satelliti. Due sfere si intersecano lungo un cerchio, tre sfere si intersecano in due punti e quattro sfere possono avere in comune uno ed un sol punto. Come nel caso dei cerchi di altezza, nel caso di tre sfere possiamo ugualmente ottenere la posizione se siamo in grado di escludere uno dei due punti d'incontro, perchè irragionevolmente lontano dalla nostra posizione presunta o perchè cade dentro la Terra o al di fuori di essa. Se usiamo quattro satelliti possiamo ottenere la posizione dell'osservatore senza alcuna ambiguità, anche se si trova nello spazio. Poichè la strumentazione attuale fornisce la distanza con grande rapidità, la variazione della distanza nel tempo permette di conoscere la direzione e la velocità con cui si muove l'osservatore sulla Terra o nello spazio.
Torna alla pagina principale del Cielo dei Navigatori