Da Commissione Divulgazione - Unione Astrofili Italiani.

Indice 1 Il sistema Alto-azimutale 2 Pietro Apiano 3 Aprile 4 Agosto 5 ABU RAIHAN AL-BIRUNI 6 Boote 7 La geometria delle proiezioni cartografiche 8 Claudio Tolomeo Cartografo 9 Isole Cassiteridi 10 Il primo viaggio di Colombo 11 Il primo approdo di Colombo - La teoria dell'Isola Watlings 12 Quanto erano lunghe le leghe usate da Colombo? 13 Colombo e la longitudine 14 Il Concilio dell'Unione 15 Poesia, Astronomia e Geografia in Dante 15.1 Il tramonto a Gerusalemme 15.2 Il sorgere del Sole a Gerusalemme 16 Dicembre 17 Didascalia delle nostre cartine 18 Testimonianze astronomiche in Toscana: il grande gnomone della Cattedrale di Santa Maria del Fiore a Firenze 19 Un'esperienza didattica: calcolo della latitudine e della longitudine 20 Le eclissi di Luna e la longitudine 21 Il Sistema Equatoriale assoluto 22 Il sistema di riferimento equatoriale relativo 23 Equazione del Tempo e Tempo civile 24 Feaci 25 Febbraio 26 Breve storia dei fusi orari 27 L'orologio H1 28 L'orologio H2 29 L'orologio H3 30 L'orologio H4 31 AL-IDRISI 32 Gennaio 33 Luglio 34 Giugno 35 Lamo 36 LEAP SECOND ALERT! 37 Le coordinate geografiche 38 Il cielo è diverso se osservato da luoghi diversi della Terra 39 Marzo 40 Maggio 41 Meridiani 42 Il Notturnale 43 L'orologio notturno per la longitudine di Firenze (può funzionare in qualunque luogo) 44 Novembre 45 Scale non rotazionali 46 Ottobre 47 Ogigia 48 Paralleli 49 Pitea, esploratore avventuroso (e fantasioso) del IV secolo a.C. 50 Pleiadi 51 La Precessione degli Equinozi 52 Le proiezioni prospettiche 53 Rallentamento della velocità di rotazione della Terra 54 Scale rotazionali

Il sistema Alto-azimutale

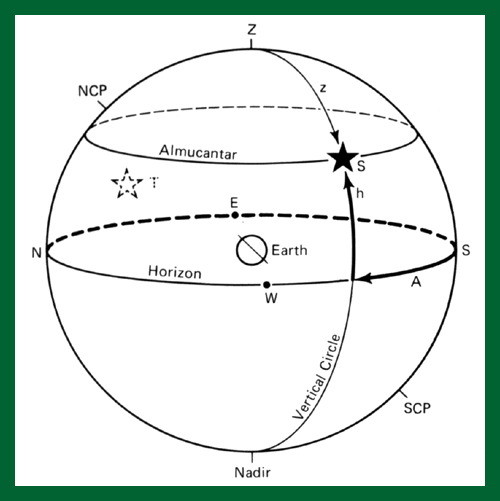
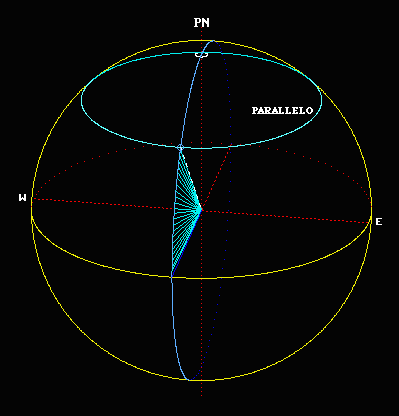
Il sistema alto-azimutale è il sistema di riferimento più vicino alla nostra esperienza quotidiana, corrisponde pressappoco alle indicazioni più su, più giù oppure a destra, a sinistra che siamo abituati a dare ad un interlocutore, per indicare un qualche oggetto in cielo. Il piano fondamentale di questo sistema è il piano orizzontale definibile in maniera operativa mediante un filo a piombo o una semplice livella. Il piano origine è invece il piano meridiano che è quel piano verticale che passa per i punti Nord e Sud dell'orizzonte.

Le due coordinate di questo sistema sono l'altezza, che è l'angolo sotteso dall'arco h, e l'azimut, che è l'angolo sotteso dall'arco A. In ambito astronomico l'azimut viene misurato in senso orario, a partire dal punto Nord dell'orizzonte. In ambito topografico viene anche misurato a partire da Sud. Per questo è importante dichiarare sempre quale convenzione si adotta. Noi seguiremo la prima, cioè conteremo gli azimut da Nord verso Est, in senso orario. I cerchi minori, paralleli al piano orizzontale, prendono il nome di almuncantarat. I cerchi massimi, generati come intersezioni con la sfera celeste dai piani verticali passanti per lo zenit, come ZS, prendono il nome di cerchi verticali. L'altezza del Polo Nord celeste, NCP, è pari alla latitudine del luogo, e quindi cambia se ci si sposta in latitudine sulla superficie terrestre. Al Polo Nord terrestre, il Polo Nord celeste coincide con lo zenit, all'Equatore invece il Polo Nord celeste si trova sull'orizzonte e coincide con il punto cardinale Nord.

Il sistema di riferimento alto-azimutale non è particolarmente adatto per descrivere in maniera semplice le posizioni degli astri in cielo. Per questo motivo sono stati sviluppati i sistemi equatoriale relativo e equatoriale assoluto.

[Per tornare alla pagina precedente usare il bottone back del browser]

Pietro Apiano

Peter Bienewitz, detto Apiano (Leisnig 16 Aprile 1495 - Ingolstadt 21 Aprile 1552) fu un abile costruttore di strumenti e un bravo divulgatore di Astronomia. I suoi lavori ebbero molta fortuna nel XVI secolo. Tra le sue opere più importanti c'è la Cosmografia, basata sulla Geografia di Claudio Tolomeo. L'opera risultò un manuale di Geografia Astronomica e di Astronomia, facilmente leggibile. Il grande successo di pubblico per questo lavoro gli procurò la cattedra di Astronomia ad Ingolstadt e il titolo di cavaliere da parte di Carlo V. Nella Cosmografia Apiano suggerisce il metodo delle distanze lunari per valutare il tempo siderale del meridiano di riferimento del sistema di longitudini terrestri.

Per osservare le distanze lunari suggerì l'uso della balestriglia. Proprio per rendere più agevole l'uso di questo strumento, pubblicò una tavola di funzioni trigonometriche, con il passo di un minuto d'arco.

[Per tornare alla pagina precedente usare il bottone back del browser]

Aprile

Aprile: l'arrivo della primavera rinnova la vita e la speranza, l'erba è verde e due promessi sposi si scambiano gli anelli, accompagnati dagli amici e dai parenti....

[Per tornare alla pagina precedente usare il bottone back del browser]

Agosto

Agosto: è tempo di caccia per i nobili mentre i contadini continuano a lavorare nei campi e si concedono un po' di svago nuotando nel fiume.

[Per tornare alla pagina precedente usare il bottone back del browser]

ABU RAIHAN AL-BIRUNI

Abu Raihan Mohammad Ibn Ahmad al-Biruni (973-1048 d.C.) fu uno scienziato e uno studioso molto versatile, al seguito del suo sultano passò un periodo di circa venti anni in India e imparò la lingua di quel paese. Al suo ritorno dall'India, scrisse un famoso libro in cui discusse diversi teoremi di astronomia e trigonometria e le caratteristiche del moto della Luna del Sole e dei pianeti. Nello stesso libro discusse della rotazione della Terra e fornì valori molto precisi delle coordinate geografiche di vari luoghi. Al-Biruni è considerato giustamente un grande scienziato dell'Islam ed uno dei più grandi tra quelli vissuti in tutti i tempi. In lui lo spirito critico, l'amore per la verità e l'approccio scientifico ai problemi era accompagnato da una grande tolleranza e saggezza. Il suo entusiasmo per la scienza è testimoniato dalla frase che amava ripetere Allah è onnisciente, e non giustifica l'ignoranza.

[Per tornare alla pagina precedente usare il bottone back del browser]

Boote

Boote, è una delle costellazioni più importanti dell`emisfero settentrionale, la osserviamo bene in Primavera e nella prima parte dell`Estate. La leggenda identifica Boote con l'ateniese Icario che aveva come figlia Erigone. Avendo Icario appreso da Dioniso (Bacco per i romani) l'arte di fare il vino, pensò di offrire la nuova bevanda a dei contadini i quali, ubriacatisi lo uccisero. La figlia Erigone andò in giro per il mondo a cercare la tomba del padre aiutata da Maira, il cane del padre. Trovatala si uccise, impiccandosi, per il dolore. Giove impietosito assunse in cielo Boote ed Erigone che, a sua volta, diventò la costellazione della Vergine. Maira invece divenne Procione, la stella più luminosa della costellazione del Cane Minore.

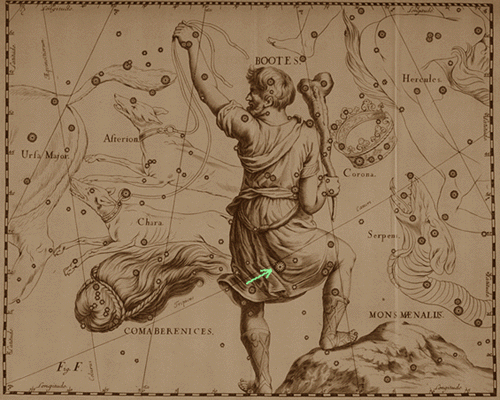
La costellazione del BOOTE da Johann Hevelius: URANOGRAPHIA (1690) (la freccia indica la stella Arturo). L'immagine appartiene alla collezione storica del Museo astronomico di Brera, disponibile in rete . Nella cartografia celeste dell'epoca i punti cardinali Est ed Ovest risultano invertiti in quanto il cielo viene rappresentato come un globo celeste visto dall'esterno. Appartiene alla costellazione di Boote la stella Arturo che è la quarta stella in ordine di luminosità del cielo. Arturo si trova alla distanza di 36 anni luce (ci vogliono cioè 36 anni perché la luce di Arturo giunga fino a noi). Si pensa che abbia la stessa massa del Sole, ma ha un diametro più grande di 27 volte.

[Per tornare alla pagina precedente usare il bottone back del browser]

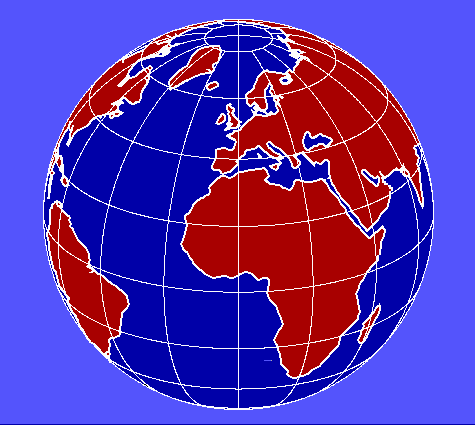
La geometria delle proiezioni cartografiche

Ci sono diversi metodi per realizzare le carte geografiche. Si sceglie l'uno o l'altro a seconda della localizzazione sulla Terra della superficie terrestre che si vuol rappresentare e delle proprietà che si vogliono conservare. Tutti i metodi, comunque, derivano da un'operazione geometrica detta proiezione. Una sfera (o una porzione di essa) può essere proiettata su un piano in due soli modi, il che ci permette così di classificare le proiezioni in:

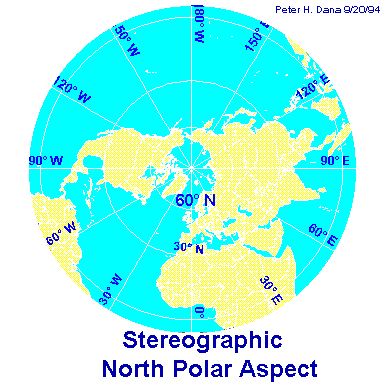
Proiezioni prospettiche o azimutali

Proiezioni per sviluppo Nelle proiezioni prospettiche il piano di proiezione può essere tangente o secante ed in quest'ultimo caso passare o no per il centro della sfera.

Lungo la retta pependicolare al piano di proiezione e passante per il centro della sfera viene fissato il punto di vista. Da esso si tracciano le congiungenti con i punti della Terra che si vogliono rappresentare; le loro intersezioni con il piano costituiscono la carta geografica. La posizione del punto di vista permette di costruire differenti proiezioni azimutali.

Nelle proiezioni per sviluppo la Terra viene avvolta da una superficie conica o cilindrica che può essere tangente o secante e viene scelto un opportuno punto di vista che, generalmente, coincide con il centro della sfera. Una volta che i vari punti della Terra sono stati proiettati, la superficie viene svolta e si ottiene la carta geografica piana.

Il cilindro può essere tangente o secare la Terra lungo l'equatore (Proiezioni Normali), lungo un meridiano (Proiezioni Trasverse) o lungo un cerchio qualsiasi (Proiezioni Oblique).

Anche in questo caso la posizione del punto di vista permette di realizzare differenti proiezioni per sviluppo

Dobbiamo la gran parte delle immagini usate in questa pagina ed in quelle ad essa correlate a Peter H. Dana, docente presso il Department of Geography, University of Texas at Austin che è autore di interessanti lezioni sull'argomento all'indirizzo:

Map Projection

[Per tornare alla pagina precedente usare il bottone back del browser]

Claudio Tolomeo Cartografo

Schema della proiezione adottata da C. Tolomeo, riportata in una traduzione latina della "Geografia" Claudio Tolomeo può essere considerato a buon diritto l'iniziatore della cartografia scientifica. Nella prima proiezione da lui adottata i meridiani sono disegnati come raggi di circonferenza che si incontrano in un punto H che però non è il Polo Nord. I paralleli sono archi di cerchio che hanno H come centro. L'equidistanza è conservata attorno al parallelo e al meridiano di Rodi, come pure si conserva il rapporto tra la lunghezza del grado di longitudine, alla latitudine di Rodi e alla latitudine di 63° Nord. Tolomeo modifica la proiezione a sud dell'Equatore per meglio rappresentare le terre note in questa zona. In termini moderni la proiezione di Tolomeo può essere classificata come una proiezione conica secante, modificata. Possiamo dire che Tolomeo compì un passo da gigante nella teoria della costruzione delle carte geografiche, che rimase insuperato per almeno 1.400 anni, anche se le descrizioni dei luoghi e le posizioni in alcuni casi erano grossolanamente sbagliate o molto approssimate.

[Per tornare alla pagina precedente usare il bottone back del browser]

Isole Cassiteridi

Sono delle isole poste sulla coste occidentali dell'Europa. Il nome deriva dalla parola greca che indica lo stagno. Le isole dovevano essere luoghi dove si ricavava, appunto, lo stagno. Erodoto (430 a.C.) non ne conosceva esattamente l'ubicazione. Diodoro siculo le poneva vicine alla costa della Spagna. Studi archeologici recenti hanno dimostrato che i Fenici e i Greci ricavavano lo stagno dalle coste della Spagna e della Cornovaglia. Attualmente si tende ad identificare le isole Cassiteridi con le isole che si trovano vicino alle coste bretoni. Comunque, nel linguaggio omerico significavano probabilmente un luogo oltre le Colonne d'Ercole e verso settentrione.

[Per tornare alla pagina precedente usare il bottone back del browser]

Il primo viaggio di Colombo

Il diario di bordo originale del primo viaggio non ci è pervenuto, comunque ne abbiamo un ottimo estratto scritto nel 1530 da Bartolomeo de Las Casas. Partito dal porto di Palos (vicino Huelva) in Spagna, Colombo si dirige alle Isole Canarie, l'ultimo possedimento spagnolo verso ovest. dove si trattiene per quattro settimane a causa di una calma di venti e per la necessità di eseguire riparazioni. Colombo lascia l'isola di Gomera il 6 settembre 1492, ma la bonaccia dopo la partenza lo lascia in vista dell' isola di Hierro, la più occidentale delle Canarie, fino all'8 settembre. Nel viaggio verso ovest, Colombo registra due serie di distanze nel suo diario, secondo La Casas questo fu fatto per nascondere ai marinai l'esatta distanza percorsa. Probabilmente le due registrazioni sono dovute al fatto che Colombo registrava le distanze percorse in leghe italiane (2.67 miglia nautiche) e in leghe portoghesi (3.19 miglia nautiche). Tra le due unità di misura esiste un rapporto di 1.2 ed è significativo che le due serie di registrazioni stiano proprio in questo rapporto. Comunque, nella storiografia colombiana, esiste il problema di capire quale fosse realmente la lunghezza della lega utilizzata.

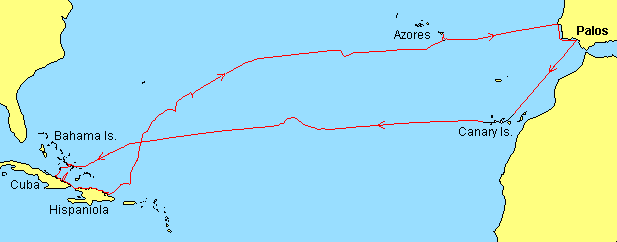
La rotta seguita da Colombo nel primo viaggio Colombo arriva al tuttora incerto primo approdo nelle Bahamas il 12 ottobre, quindi procede verso Cuba (28 ottobre) e Hispagnola (1 Dicembre). L'ammiraglia Santa Maria si incaglia su di una scogliera la vigilia di Natale e affonda il giorno dopo. Colombo ritorna in Spagna con la Nina, lasciando la baia di Samana (nell'attuale Repubblica Domenicana) il 16 gennaio 1493 e avvista l'isola di Santa Maria, nelle Azzorre, il 15 febbraio. Dopo un incontro con il governatore locale, arriva a Lisbona il 4 marzo e finalmente ritorna a Palos il 15 Marzo.

Per ulteriori approfondimenti consultare in rete:

The First Voyage of Columbus

[Per tornare alla pagina precedente usare il bottone back del browser]

Il primo approdo di Colombo - La teoria dell'Isola Watlings

Per gran parte del XIX e XX secolo si è pensato che il primo sbarco di Colombo fosse avvenuto nell'isola di Watlings. Nel 1926 la storica Ruth Wolper convinse anche il parlamento delle Bahamas a ribattezzare ufficialmente l'isola di Watlings in San Salvador, nome con cui è indicata in molte carte odierne. Tuttavia ci sono numerosi luoghi in cui Colombo potrebbe essere approdato per la prima volta e diversi sono gli itinerari proposti per gli spostamenti successivi. Infatti, anche la più accettata localizzazione dell'isola di primo approdo non corrisponde perfettamente con le descrizioni di Colombo:

Nessuna rotta transatlantica è compatibile con la linea lossodromica WSW fra Hierro e Dominica, che Colombo segue nel secondo viaggio; per mantenere la compatibilità il punto di approdo deve essere spostato verso Sud. Colombo riporta che vi era una scogliera che circondava completamente l'isola. La scogliera non circonda completamente Watlings e Colombo doveva esserne a conoscenza Colombo menziona un'entrata attraverso la scogliera "molto stretta". A Watlings l'interruzione della scogliera è larga 1400 metri Colombo riferisce di vedere molte isole a distanze diverse dopo aver lasciato la prima isola, alcune più vicine di 5 leghe. Da Watlings è visibile solo Rum Cay, ed è più lontana di 5 leghe. La seconda isola aveva una costa N-S di 5 leghe. La costa N-S di Rum Cay è meno di 2 leghe. Colombo dice che la costa N-S della seconda isola è di fronte alla prima isola. La costa N-S di Rum Cay non si affaccia su Watlings. Colombo riporta che la seconda isola ha una costa E-W di più di 10 leghe. La costa di Rum Cay è meno di 4 leghe. Colombo riporta che per andare dalla seconda isola alla terza, naviga verso W. La direzione da tenere per andare da Rum Cay a Long Island è WSW Colombo riporta che la distanza fra la seconda e la terza isola è di 8 o 9 leghe. La distanza fra Rum Cay e Long Island è di 6 leghe. Gli storici hanno cercato di risolvere tutte queste incertezze spostando il punto di primo approdo lungo tutte le isole dei Caraibi, senza trovare un'isola che soddisfi a tutte le indicazioni. Per questo, nonostante i problemi che abbiamo accennato, l'isola di Watlings rimane tuttora la candidata preferita ad essere il primo approdo di Colombo nel Nuovo Mondo.

[Per tornare alla pagina precedente usare il bottone back del browser]

Quanto erano lunghe le leghe usate da Colombo?

Sul mare Colombo misurava le distanze in leghe, ognuna delle quali era lunga 4 miglia, ma nel quindicesimo secolo erano in uso diverse unità di misura sotto lo stesso nome di lega e di miglio. Questo fa nascere ambiguità su quanto dovessero essere lunghi la lega e il miglio usati da Colombo. Samuel E. Morrison assume che Colombo usi il miglio romano di 1481 metri, questo porta la lega ad essere lunga 3,2 miglia marine, che è la lunghezza accettata per la Lega Marittima Portoghese (LMP), di uso comune fra i marinai portoghesi e spagnoli. Tuttavia l'interpretazione delle misure fornite da Colombo in termini di LMP presenta numerosi problemi. Per esempio, se cerchiamo di controllare le distanze riportate da Colombo fra punti identificabili quando segue la costa nord di Cuba, si trova che tutte le distanze reali sono minori di quelle indicate. Inoltre, se accettiamo il primo approdo all'isola di Watlings, ci sono molte lunghezze di linee costiere delle varie isole che risultano enormemente sovrastimate. Per risolvere questi problemi Morrison suggerisce che Colombo, per misurare le linee costiere, usi leghe di minore lunghezza (1,5 miglia nautiche), ma non esistono né indicazioni, né ragioni a favore di questa ipotesi. Inoltre, se si cerca di tracciare i viaggi transatlantici di Colombo, usando le LMP è impossibile far tornare le distanze, se non si fa uso di strani e ingiustificati fattori di riduzione delle medesime. Altri ricercatori fanno notare che Colombo era genovese e in Italia, nel quindicesimo secolo, si usava comunemente un miglio più corto, il Miglio Italiano o Geometrico di 1237 metri. Se Colombo usa il miglio italiano la sua lega, o Lega Geometrica (LG), sarebbe stata di 2,67 miglia marine. Se si usa questa lunghezza per la lega, gran parte delle difficoltà si risolvono automaticamente. Per questo motivo l'uso della LG da parte di Colombo ha largamente acquisito attendibilità fra gli storici.

Per ulteriori approfondimenti su questo argomento consultare in rete:

How long was Columbus's league?

[Per tornare alla pagina precedente usare il bottone back del browser]

Colombo e la longitudine

Colombo fece due tentativi, durante la sua vita, di misurare la longitudine a cui si trovava. Entrambi i risultati furono del tutto deludenti. L'unico modo per determinare la longitudine nel quindicesimo secolo era il metodo basato sulla determinazione dei tempi locali delle varie fasi di eclissi lunari. Questo metodo era noto dai tempi antichi, ma a causa della rarità delle eclissi, di uso molto limitato.

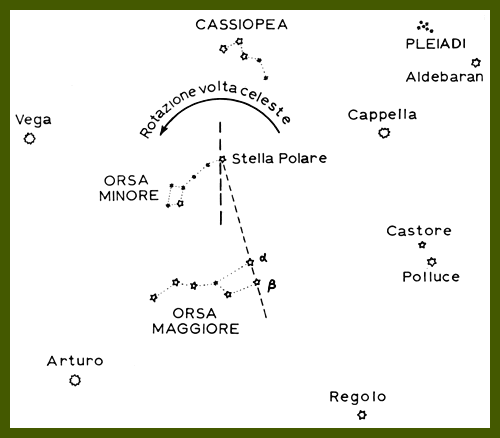
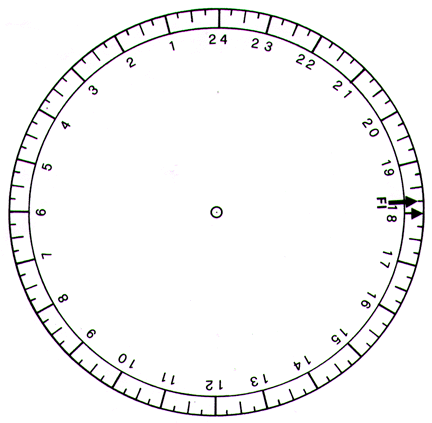
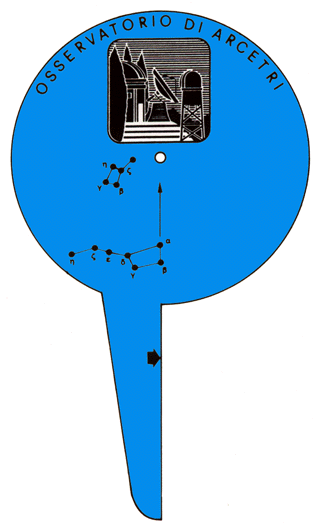
Ai tempi di Colombo, osservatori accorti potevano ottenere l'ora locale con una precisione di pochi minuti. Questo poteva essere fatto abbastanza facilmente con l'uso di uno strumento, chiamato notturnale, con cui era possibile determinare la mezzanotte locale, od altro momento della notte, dalla posizione delle stelle circumpolari.

Usando queste informazioni e una clessidra a sabbia, Colombo doveva essere in grado di determinare correttamente l'ora locale delle varie fasi di un'eclisse lunare, con la precisione di circa dieci minuti. Ma entrambe le determinazioni di longitudine, eseguite da Colombo con il metodo delle eclissi, risultarono errate di una quantità di gran lunga superiore a questa precisione. La misura eseguita nel 1494 dette come risultato una longitudine di 5 ore e 23 minuti ad Ovest di Cadice, mentre sarebbe dovuta essere di 4 ore e 10 minuti, con un errore di 1 ora e 13 minuti. L'errore nella misura del 1504 è ancora maggiore: in Giamaica determinò una longitudine di 7 ore e 20 minuti ad Ovest di Cadice, mentre l'esatto valore sarebbe dovuto essere 4 ore e 45 minuti, con un errore di oltre 2 ore e mezzo!

Il modo migliore per spiegare questi errori è di assumere che Colombo in realtà non usasse per niente le eclissi lunari. Noi sappiamo che Colombo credeva che un grado sulla superficie terrestre corrispondesse a 56 miglia e 2/3. Usando questo valore è possibile convertire la lunghezza del viaggio transatlantico misurata da Colombo (1142.25 leghe) in una misura di longitudine. Quando si fa questa conversione si trova una differenza di longitudine proprio di 5 ore e 23 minuti, l'esatto valore riportato come misurato con il metodo dell'eclissi, nel secondo viaggio.

La misura del 1504 può essere spiegata in una maniera simile. Nel suo quarto viaggio Colombo riporta che la distanza fra Porto Rico e una località sulla costa occidentale di Cuba era di 400 leghe. Questa è la massima distanza Est-Ovest che Colombo registra nella sua vita. Se aggiungiamo queste 400 leghe alla lunghezza del primo viaggio (la maggiore distanza transatlantica mai misurata da Colombo) otteniamo 1542.25 leghe. Convertendo questa distanza in longitudine, usando il valore del grado di longitudine secondo Colombo, si ottiene appunto 7 ore e 15 minuti, esattamente quanto riportato nel giornale di bordo.

Secondo questa ipotesi, Colombo usa le sue distanze, ottenute con metodi tradizionali, e dichiara che sono state determinate con metodi astronomici. Tutto ciò, probabilmente, per dare un'immagine di rispettabilità scientifica alle sue misure.

[Per tornare alla pagina precedente usare il bottone back del browser]

Il Concilio dell'Unione

Nel 1438 si aprì a Ferrara il Concilio dell'Unione che, nell'intenzione dei suoi promotori, doveva servire a gettare un ponte tra la Chiesa d'oriente e quella di occidente, anche in vista della forte pressione esercitata dai Turchi sulla città di Costantinopoli. In seguito sarà possibile apprezzare quale grande importanza questo evento abbia avuto nella storia della nostra cultura. L'apertura del Concilio era attesa con trepidazione degli umanisti i quali si aspettavano che la delegazione proveniente da Costantinopoli portasse chissà quali importanti manoscritti di argomento non solo filosofico ma anche scientifico. Quando nel 39 il Concilio si trasferì a Firenze, esso venne accolto in città dal cancelliere della repubblica, Leonardo Bruni, con un discorso in greco.

Patriarca Giuseppe della Chiesa d'oriente al suo arrivo a Firenze (Dagli affreschi di Benozzo Gozzoli in palazzo Medici Riccardi a Firenze)

Anche se i frutti del Concilio sull'argomento dell'incontro delle Chiese furono piuttosto effimeri, dal punto di vista culturale il Concilio ebbe una grandissima influenza. Si narra che Cosimo il Vecchio ascoltando le lezioni del grande Gemisto Pletone abbia deciso di fondare nella villa di Careggi l'accademia Platonica. Il Pletone non parlava solo delle contrapposizioni esistenti tra la filosofia di Platone e di Aristotele, i suoi interessi toccavano anche la geografia; infatti conosceva bene la Geografia di Claudio Tolomeo ed aveva una predilezione particolare per Strabone.

Giovanni VII paleologo, sovrano dell'Impero Romano d'oriente (Dagli affreschi di Benozzo Gozzoli in palazzo Medici Riccardi a Firenze).

Durante il Concilio si presentarono a Firenze anche singolari personaggi come quel Niccolò de' Conti che si era dovuto convertire alla fede islamica durante un lunghissimo viaggio in oriente e in Egitto per salvare se e la propria famiglia. Partendo da Damasco Niccolò de' Conti aveva attraversato l'India e la Birmania, per poi toccare il Borneo, Giava e Sumatra. Sempre nello stesso periodo arrivò a Firenze anche una delegazione di Etiopi per parlare con il Pontefice che in quel periodo risiedeva in Santa Maria Novella. Tutte queste informazioni furono condensate nel portolano numero 1 conservato presso la Biblioteca Nazionale Centrale di Firenze e il mappamondo di Fra Mauro Camaldolese, datato 1459, conservato presso la biblioteca Marciana di Venezia e che si trova in copia presso il Museo di Storia della Scienza a Firenze.

Dunque il Concilio dell'Unione fu, per la cultura occidentale, un importante momento di incontro tra la cultura medioevale e quella orientale ed ellenistica. Contemporaneamente, almeno per quanto riguarda la Geografia, fu possibile arricchire i testi con nuove informazioni prevenienti dai viaggiatori che il Concilio aveva richiamato a Firenze. Frutto di questa elaborazione culturale sarà il supporto teorico dato da Maestro Paolo alla grande impresa di Colombo.

[Per tornare alla pagina precedente usare il bottone back del browser]

Poesia, Astronomia e Geografia in Dante

Il tramonto a Gerusalemme

Già era `l Sole a l'orizzonte giunto lo cui meridian cerchio coverchia Ierusalem col suo più alto punto; e la Notte, che opposita a lui cerchia, uscia di Gange fuor con le Bilance, che le caggion di man quando soverchia; sí che le bianche e le vermiglie guance, la' dov' i 'era, de la bella Aurora, per troppa etate divenivan rance. (Purg. II, 1-9)

Le prime due terzine ci dicono che il Sole era giunto all'orizzonte ovest di Gerusalemme (e quindi stava tramontando) e la Notte, intesa come un astro buio opposto al Sole, che gira intorno alla Terra sempre in opposizione ad esso, usciva dal Gange in congiunzione con la Bilancia; ovvero stava salendo dall'orizzonte est di Gerusalemme insieme al segno della Bilancia, che è opposto a quello dell'Ariete dove si trovava il Sole durante il viaggio dantesco. Nell'estremo oriente (Gange) è mezzanotte, nell'estremo occidente è mezzogiorno (anche se Dante questo non lo dice). Da tutto il quadro risulta che a Gerusalemme sono le diciotto di tempo solare locale. È comunque sempre così al momento del tramonto il giorno dell'equinozio. Tralasciamo l'interpretazione del verso "che le caggion di man quando soverchia ", perchè è dubbia e in ogni caso non è rilevante per il nostro discorso. Passiamo all'ultima terzina, che si riferisce al Purgatorio dove Dante si trovava: siamo agli antipodi di Gerusalemme, quindi l'orizzonte astronomico è lo stesso, ma le direzioni Est e Ovest sono scambiate tra loro. Qui è il Sole che sta sorgendo e sono le sei di mattina: l'Aurora, altra creatura mitologica, ha superato lo stadio del colore bianco e poi vermiglio ed ora è arancione (siamo ormai allo spuntar del Sole). Dante continua nella sua descrizione:

Il sorgere del Sole a Gerusalemme

Si' come quando i primi raggi vibra la' dove il suo fattor lo sangue sparse, cadendo Ibero sotto l'alta Libra, e l'onde in Gange da nona riarse, si' stava il Sole; onde 'l giorno sen giva, come l'angel di Dio lieto ci apparse. (Purg. XXVII, 1-6)

Il Sole era nella posizione in cui i suoi raggi cominciano ad arrivare a Gerusalemme (il luogo dove il suo creatore, il Cristo, sparse il proprio sangue), mentre l'estremo occidente (Ibero sta per Ebro e quindi Spagna) aveva al meridiano la Bilancia (e quindi la Notte), e l'estremo oriente (Gange) aveva al meridiano il Sole: per cui al Purgatorio era il tramonto, quando ci apparve lieto l'angelo di Dio. Adesso sono le 6 di tempo solare locale a Gerusalemme e le 18 al Purgatorio, mezza notte sulla Spagna e mezzogiorno (ora in cui si ha l'inizio della nona liturgica) sul Gange. Rispetto alla situazione precedente si sono scambiati fra loro di posto il Sole e la Notte, e questa volta, con due terzine soltanto, viene data l'ora per tutti e quattro i meridiani fondamentali.

[Per tornare alla pagina precedente usare il bottone back del browser]

Dicembre

Dicembre: Non c'è più molto da fare nei campi. l'unica attività all'aperto è la caccia. È stata catturata una grossa preda: un cinghiale.

[Per tornare alla pagina precedente usare il bottone back del browser]

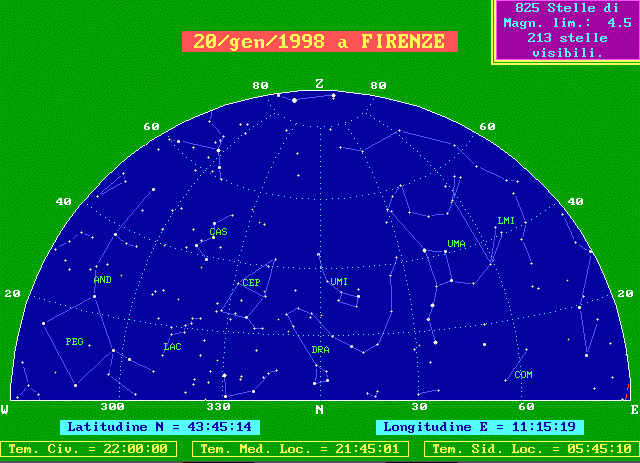
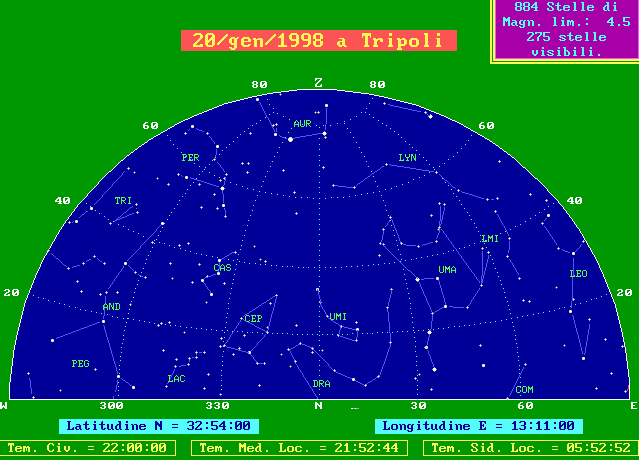
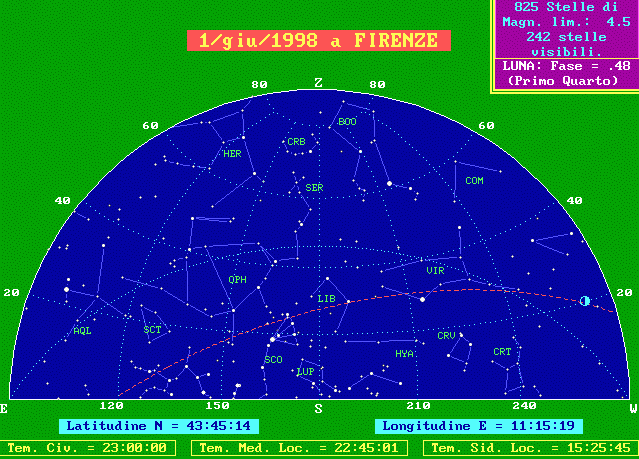
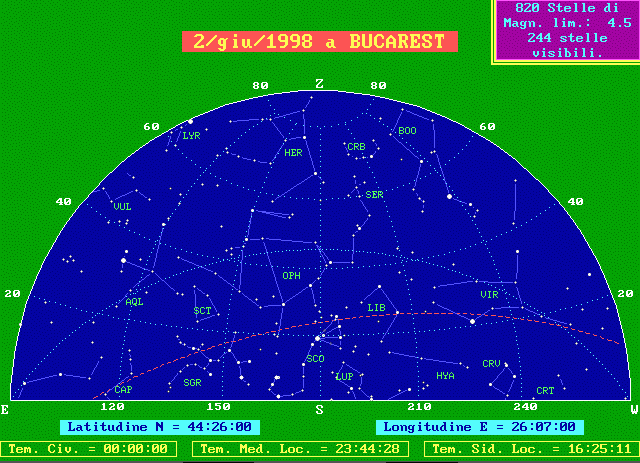
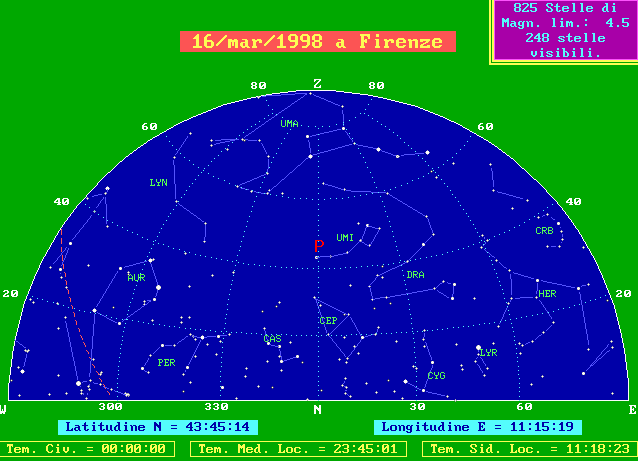
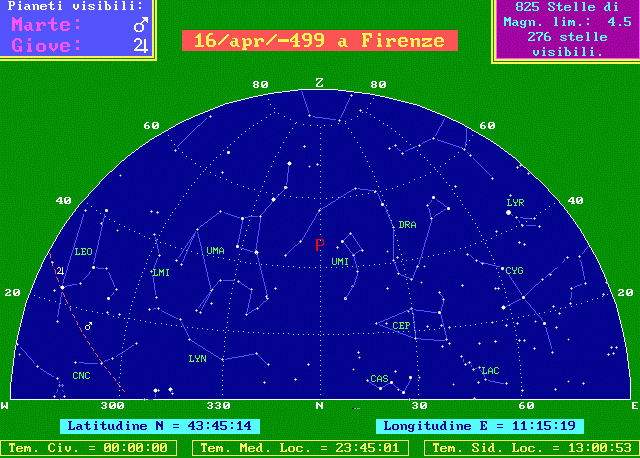
Didascalia delle nostre cartine

Quando si osserva il cielo, specie se l'orizzonte è sgombro, si ha la sensazione di essere al di sotto di una cupola semisferica, poggiata sul grande circolo dell'orizzonte. Le cartine la rappresentano divisa in due parti, ognuna centrata nel punto cardinale indicato al centro del disegno in basso. Da una parte e dall'altra gli altri due punti cardinali ed in alto lo Zenit. Nel disegno sono presenti, sullo sfondo, talvolta il reticolato delle coordinate alto-azimutali, con i cerchi di altezza di 20° in 20° e quelli di azimut di 30° in 30°, talvolta il reticolato delle coordinate equatoriali con i cerchi di declinazione di 20° in 20° e quelli di angolo orario di 2 ore in due ore. L'altezza è misurata dall'orizzonte allo zenit da 0° a 90° e l'azimut da Nord verso Est, in senso orario, da 0° a 360°. La graduazione di altezza ed azimut è indicata lungo il bordo delle cartine. Le stelle sono rappresentate con 5 simboli decrescenti al crescere della magnitudine, cioè al diminuire della luminosità apparente. Non sono rappresentate tutte le stelle conosciute, nè tutte quelle visibili ad occhio nudo, ma solo quelle più luminose della magnitudine 4.5 che è la magnitudine limite delle cartine. Il riquadro in alto a destra riporta il numero delle stelle visibili, cioè sopra l'orizzonte e quindi presenti nei due quarti di sfera che rappresentano tutto il cielo. Sono state disegnate schematicamente le costellazioni secondo la tradizione iconografica più diffusa. I loro nomi, abbreviati con la sigla in uso nei cataloghi stellari, sono qui sotto riportati per esteso: AQR Acquarius AND Andromeda ANT Antlia APS Apus AQL Aquila ARA Ara ARI Aries AUR Auriga BOO Bootes CAE Caelum CAM Camelopardus CNC Cancer CVN Canes Venatici CMA Canis Major CMI Canis Minor CAP Capricornus CAR Carina CAS Cassiopea CEN Centaurus CEP Cepheus CET Cetus CHA Chamaeleon CIR Circinus COL Columba COM Coma Berenices CRA Corona Austrina CRB Corona Borealis CRV Corvus CRT Crater CRU Crux CYG Cygnus DEL Delphinus DOR Dorado DRA Draco EQU Equuleus ERI Eridanus FOR Fornax GEM Gemini GRU Grus HER Hercules HOR Horologium HYA Hydra HYI Hydrus IND Indus LAC Lacerta LEO Leo LMI Leo Minor LEP Lepus LIB Libra LUP Lupus LYN Lynx LYR Lyra MON Monoceros MUS Musca NOR Norma OCT Octans OPH Ophiuchus ORI Orion PAV Pavo PEG Pegasus PER Perseus PHE Phoenix PIC Pictor PSC Pisces PSA Piscis Austrinus PUP Puppis PYX Pyxis RET Reticulum SGE Sagitta SGR Sagittarius SCO Scorpius SCL Sculptor SCT Scutum SER Serpens SEX Sextans TAU Taurus TEL Telescopium TRI Triangulum TRA Triangulum Australe TUC Tucana UMA Ursa Major UMI Ursa Minor VEL Vela VIR Virgo VOL Volans VUL Vulpecola

Il cerchio puntinato rappresenta l'equatore celeste, l'altro tratteggiato in rosso l'eclittica, cioè il cammino apparente annuo del Sole tra le stelle. Lungo l'eclittica la Luna, la cui fase è indicata nel riquadro in alto a destra, ed i pianeti, disegnati con i vecchi simboli secondo la legenda in alto a sinistra, che considera "visibili" i pianeti presenti nella cartina cui si riferisce. Completano la cartina l'indicazione della latitudine e della longitudine del luogo, del tempo civile, di quello solare medio locale e di quello siderale locale. Questi argomenti possono essere approfonditi presso i seguenti siti della rete:

Il cielo mese per mese Le costellazioni negli antichi atlanti celesti

[Per tornare alla pagina precedente usare il bottone back del browser]

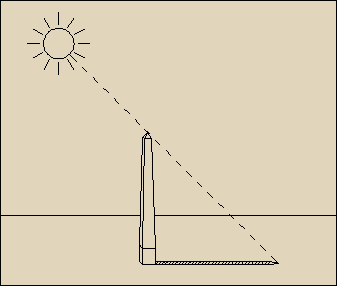
Testimonianze astronomiche in Toscana: il grande gnomone della Cattedrale di Santa Maria del Fiore a Firenze

Il Duomo di Firenze ospita, fin dalla sua costruzione, un grande strumento astronomico, uno gnomone che, con i suoi 90 metri di altezza, e' il piu' grande del suo genere e che, con alterne vicende, e' stato utilizzato in programmi scientifici per oltre 300 anni. Uno gnomone, e' un palo, una colonna, un obelisco la cui ombra permette di misurare la posizione del Sole in cielo. Lo gnomone, nella sua semplicita' tecnologica, e' sicuramente lo strumento astronomico piu' antico e diffuso; con esso si poterono ben presto studiare i due moti apparenti del Sole, quello diurno e quello annuo, dovuti rispettivamente ai moti reali di rotazione e rivoluzione della Terra. Fu ben presto chiaro che l'accuratezza della misura poteva essere aumentata usando pali sempre piu' alti, cioe' aumentando l'altezza dello gnomone. Poiche' il Sole e' una sorgente estesa che sottende un angolo di circa 1/2 grado in cielo, l'ombra del vertice dello gnomone non e' nitida, ma sfuma in una penombra mal definita. Purtroppo il contrasto tra ombra, penonmbra e superficie illuminata diminuisce rapidamente con l'aumentare dell'altezza dello gnomone e pone un serio limite all'accuratezza che, per questa via, si puo' ottenere. Il modo piu' efficace per aumentare il contrasto e' di sostituire l'ombra con la luce e cioe' di usare un foro gnomonico al posto del palo, come e' stato fatto in S. Maria del Fiore e negli altri gnomoni rinascimentali. Se il diametro del foro e' all'incirca 1/1000 dell'altezza dello gnomone si ottiene sul pavimento un'immagine abbastanza nitida del Sole, (immagine stenopeica) molto piu' luminosa della superficie circostante, ma circondata, anche in questo caso, da un alone soffuso di penombra. L'immagine stenopeica, cosi' come il vertice dell'ombra del palo si muovono continuamente da Ovest verso Est a causa del moto apparente diurno del Sole ed a questo movimento regolare si sovrappone un tremolio, sempre presente, dovuto alla turbolenza atmosferica, innescata dalle differenze di temperatura nell'aria a varie altezze, fuori e dentro l'edificio. Non c'e' modo di aumentare ulteriormente nitidezza e contrasto o di eliminare il tremolio dell'immagine se non abbandonando la semplicita' tecnologica della gnomonica e passando al telescopio. Solo nel 1700 i telescopi divengono competitivi con gli strumenti della gnomonica e si chiude allora una pagina gloriosa, iniziata qualche millennio prima; l'ultimo gnomone ad andare in pensione, scientificamente parlando, pare essere prorio quello fiorentino.

La bronzina all'interno della cupola

In S. Maria del Fiore il foro gnomonico e' stato realizzato con una tavoletta di bronzo (la bronzina) recante un'apertura centrale di un paio di centimetri di diametro e posta orizzontalmente all'interno della finestra meridionale del tamburo di cupola, a 90 metri dal pavimento. L'altezza dello gnomone e' tale che i raggi del Sole, passanti per il foro, colpiscono il pavimento della chiesa solo dalla fine di Maggio alla fine di Luglio e per pochi minuti prima e dopo il mezzogiorno. In questo periodo l'immagine solare si forma sul pavimento della Cappella della Croce, a sinistra dell'altare maggiore, dove si trovano, sotto la protezione di lastre di ottone, una linea meridiana finemente graduata e due marmi circolari, uno dentro l'altro, che funzionano da contrassegni solstiziali. Il maggiore, con un diametro di circa 90 centimetri, ha le stesse dimensioni dell'immagine solare al solstizio d'estate.

Spaccato dello Gnomone

Fino a pochi anni fa non esistevano documenti o iscrizioni che indicassero l'autore dello gnomone, la data della sua realizzazione e la problematica astronomica che si intendeva affrontare. La migliore indagine storica è, ancora oggi, quella del gesuita Leonardo Ximenes pubblicata nel 1757 come introduzione al suo volume dedicato appunto allo gnomone fiorentino. Sulla base di considerazioni cronologiche e astronomiche egli individuava in Paolo del Pozzo Toscanelli l'autore e nel 1468 la data più probabile per l'entrata in funzione dello strumento. Nel 1979 l'archivista dell'Opera del Duomo, Enzo Settesoldi, pubblica un breve articolo in cui da notizia del ritrovamento di un documento che conferma l'ipotesi dello Ximenes per quanto riguarda l'autore anche se sposta in avanti di qualche anno l'entrata in funzione. Riportiamo integralmente il documento:

Archivio dell'Opera del Duomo di Firenze Quaderno Cassa, serie VIII-1-61, anno 1475, carta 2v MCCCLXXV Spese d'Opera E adí detto (16 agosto) lire cinque soldi quindici dati a Bartolomeo di Fruosino orafo, sono per il primo modello di bronzo di libbre 23 once 4, fatto per Lui a istanza di maestro Paolo Medicho per mettere in sulla lanterna, per mettere da lato drento di chiesa per vedere il sole a certi dí dell'anno. Lire 5 soldi 15

Per quanto riguarda la problematica, sicuramente lo gnomone dovette servire ad individuare il momento esatto del solstizio e quindi a determinare la durata dell'anno tropico e dai documenti risulta che Paolo Toscanelli propose per questa grandezza un valore piu' accurato di quello usato dai contemporanei. Ma uno gnomone "cosi' smisurato" poteva servire anche per un'indagine piu' ambiziosa: determinare se l'eclittica, cioe' il cammino apparente annuo del Sole tra le stelle, si mantiene costante nel tempo; in termini moderni cio' significa determinare se l'inclinazione dell'asse della Terra, sul piano orbitale, e' costante. Questa problematica era gia' stata posta dall'astronomia araba e, successivamente, era passata a quella europea che, proprio negli anni del Toscanelli, si stava risvegliando da un torpore secolare. La questione e' chiaramente e ripetutamente enunciata a Firenze fin dai primi anni del XVI secolo e nel 1510 viene sicuramente compiuta una nuova misura, come testimonia l'iscrizione riportata sul grande marmo solstiziale. Successivamente a questa data si hanno solo sporadiche e talvolta sconclusionate osservazioni astronomiche, nessuna delle quali basata su chiari obbiettivi scientifici; anzi inizia e si protrae per quasi 250 anni un curioso uso improprio dello strumento: ipotizzando la costanza dell'altezza del Sole al solstizio si cerca di verificare la stabilita' della chiesa, osservando, anno dopo anno, il ritorno dell'immagine solare sul marmo soltiziale.

E' solo nel 1754 che si ritorna a parlare di Astronomia, quando Leonardo Ximenes formula un preciso progetto di ricerca, chiedendo ed ottenendo finanziamenti ed accesso alla chiesa ed allo gnomone. Al tempo dello Ximenes si sapeva gia' che l'asse della Terra e' soggetta ad un'oscillazione periodica con periodo 18 anni, ma non si era ancora riusciti a dimostrare che l'inclinazione dell'asse e' anche soggetta a variazioni a piu' lungo periodo che, nell'arco di un anno, sono estremamente piccole. Ma cio' che e' piccolo e forse non misurabile a distanza di un anno, puo' diventare abbastanza grande e misurabile a distanza di qualche secolo. Egli si propone di misurare questa variazione confrontando l'altezza del Sole al solstizio del 1755 con quella al solstizio del 1510, stabilmente registrata dal grande marmo, sul pavimento della cattedrale. Non e' una misura facile e lui per primo si dichiara consapevole che qualunque risultato va verificato nel tempo, con successive misure da farsi negli anni a venire. Inoltre la misura deve essere svincolata dalla cattedrale e riferita ad un sistema di coordinate, accessibile da qualunque osservatore. Per far cio' deve misurare l'altezza dello gnomone e ci riesce con un errore inferiore a qualche millimetro su 90 metri e tracciare una linea meridiana con la quale si possono apprezzare variazioni dell'altezza del Sole fino al secondo d'arco. Dopo una prima serie di misure nel 1755 e 1756 lo Ximenes torna ad usare lo strumento nel 1764 e poi nel 1782, riuscendo a dimostrare che il fenomeno esiste ed e' misurabile. Muore nel 1786 lasciando i suoi averi all'osservatorio che prendera' da lui il nome di Ximeniano, con la precisa raccomandazione al direttore di continuare le osservazioni solstiziali allo gnomone. Negli 80 anni successivi le misure sono scarse e discontinue e lo gnomone cade nell'oblio. Nel 1864 il direttore della Specola di via Romana, G. B. Donati chiede di usarlo e diventa di pubblico dominio che la bronzina non e' piu' al suo posto, essendo stata rimossa nel 1859 nel corso di alcuni lavori di restaturo. Ne parla la stampa cittadina e se ne interessa il sindaco che fa pressione sull'Opera del Duomo. G. Antonelli, direttore dell'Osservatorio Ximeniano viene incaricato di ricollocare al suo posto la bronzina che, dopo attenta e lunga ricerca, viene ritrovata nei magazzini dell'Opera e rimurata nel novembre del 1865, un po' piu' in alto, rispetto alla posizione originaria ed interrompendo cosi' ogni continuita' e possibilita' di confronto con le precedenti misure dello Ximenes. Antonelli non esegue alcuna misura e bisogna attendere il 1893 per avere una nuova serie di osservazioni (1893-1901), compiute dal nuovo direttore dello Ximeniano, Giovanni Giovannozzi che, preso atto della superiorita' dei tescopi della sua epoca, ripropone, in termini moderni, l'utilizzo delle misure sostiziali allo gnomone per la verifica della stabilita' della costruzione. Il suo successore, Guido Alfani, nel 1927-28, esegue ancora altre misure, con lo stesso scopo, e dimostra che la grande cupola e' soggetta a piccole oscillazioni, stagionali e diurne, di natura termica. Ma ormai anche l'uso ingegneristico dello gnomone viene meno e lo stesso Alfani sperimenta sismografi modificati per sorvegliare, piu' semplicemente e direttamente durante tutto l'anno, ogni piu' piu' piccola oscillazione della costruzione.

L'immagine del Sole sul pavimento di S.Maria del Fiore

Nella consapevolezza che lo gnomone aveva ormai perso ogni sua originaria utilita', Giovannozzi ed Alfani proposero l'estemporanea esecuzione delle misure sostiziali come una cerimonia per conservare nella cultura memoria dell'antico strumento, di chi lo costruì ed usò. È questa un'intuizione moderna che tante volte abbiamo visto verificata: conservazione materiale e culturale vanno di pari passo, non c'e' l'una senza l'altra. Con questo spirito gli autori di questa breve nota hanno chiesto ed ottenuto dall'Opera il permesso di eseguire nuove osservazioni per il solstizio del 1996. Non accadeva piu' dalla meta' degli anni 70 e di nuovo l'immagine del Sole si e' formata sul pavimento della Cappella della Croce ed ha attraversato la linea meridiana dello Ximenes.

---

• Questo scritto è stato tratto da un articolo che gli autori, Piero Ranfagni e Alberto Righini, hanno pubblicato nel numero di Ottobre 1996 di La Regione Toscana, periodico mensile della Giunta regionale, interamente dedicato all'Astronomia in Toscana.

[Per tornare alla pagina precedente usare il bottone back del browser]

Un'esperienza didattica: calcolo della latitudine e della longitudine

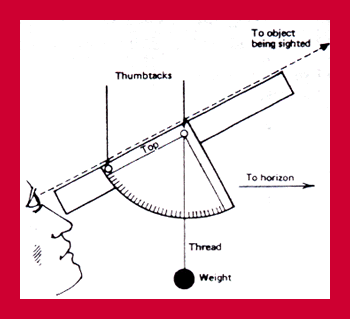
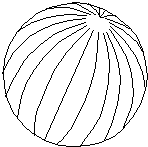
Lo scopo di questa esperienza didattica non è quello di insegnare a navigare, ma quello di chiarire operativamente il calcolo del centro e del raggio dei cerchi di altezza, utilizzando misure reali di due o più stelle, ottenute con niente di più di un goniometro ed un filo a piombo. I cerchi saranno poi disegnati su un normale mappamondo scolastico di 20-30 centimetri di raggio. Latitudine e longitudine saranno così lette direttamente sul mappamondo, con l'errore di un centinaio di chilometri, inaccettabile in mare, ma più che sopportabile nell'ambito di un'esercitazione scolastica, concettualmente rigorosa ed accessibile anche agli studenti della Scuola Media inferiore. Materiale occorrente:

Un quadrante di altezza, realizzabile semplicemente con un goniometro scolastico, una cannuccia ed un filo a piombo. Un orologio con l'ora di Greenwich, cioè un'ora indietro rispetto a quella italiana, due ore quando è in vigore l'ora legale. Un mappamondo con il diametro di almeno 30 centimetri. Un compasso da lavagne per poter tracciare i cerchi di altezza sul mappamondo Un catalogo od un atlante stellare per ottenere le coordinate equatoriali delle stelle Un annuario astronomico per il calcolo del tempo siderale.

Immaginiamo di fare la nostra esperienza il tardo pomeriggio del 20 Novembre 1998. Verso Sud vi sono due stelle facilmente riconoscibili: a Sud-Est la stella Sirrah, della costellazione di Andromeda che definisce il vertice superiore-orientale del quadrilatero del Pegaso (PEG) ed a Sud-Ovest la stella Altair, il vertice meridionale del triangolo estivo, della costellazione dell'Aquila (AQL). Consultando il catalogo o l'atlante stellare otteniamo le loro coordinate equatoriali, Ascensione Retta (AR) e Declinazione (DEC):

Stella/Coordinate AR DEC Altair 19h 50m 41s +8° 51' 47" Sirrah 00h 08m 17s +29° 04' 46"

Misuriamo l'altezza sull'orizzonte di ciascuna stella usando il quadrante d'altezza ed annotando il tempo di Greenwich (Tempo Universale, TU) corrispondente. Per ciascuna di esse dobbiamo ora calcolare le coordinate geografiche del punto substellare. Poichè equatore terrestre e celeste giacciono sullo stesso piano, la latitudine del punto substellare è uguale alla declinazione della stella:

LAT = DEC La stella culmina nel punto substellare poichè si trova al suo zenit ed il suo angolo orario (AO) vale, di conseguenza, 0h. La relazione che lega il Tempo siderale locale (TSL), l'Angolo Orario e l'Ascensione Retta

TSL = AO + AR diventa

TSL = AR Il tempo siderale locale differisce dal tempo siderale a Greenwich di una quantità pari alla longitudine (LONG) che nelle formule seguenti viene considerata positiva ad Ovest e negativa ad Est del meridiano di riferimento.

TSL = TSG - LONG TSG - LONG = AR

LONG = TSG - AR

Il Tempo siderale a Greenwich può essere facilmente calcolato a partire dal suo valore a 0h TU (TSG0h TU) e dal valore del tempo di Greenwich nel momento della misura. TSG0h TU viene fornito dagli annuari astronomici per ogni giorno dell'anno. Potete usare l'annuario dell'Osservatorio di Arcetri.

TSG = TSG0h TU + 1.00273791*TU Ora non resta che tracciare i due cerchi di altezza sul mappamondo, facendo centro nel rispettivo punto substellare e con apertura di compasso pari all'arco che sottende l'angolo al centro uguale alla distanza zenitale (Z), cioè il complemento dell'altezza misurata. L'apertura del compasso può essere ottenuta utilizzando lo stesso mappamondo e le sue graduazioni: l'arco di n gradi corrisponde alla distanza meridiana tra l'equatore e l'ennesimo parallelo. I punti d'incontro dei cerchi forniscono direttamente la latitudine e la longitudine del luogo di osservazione.

[Per tornare alla pagina precedente usare il bottone back del browser]

Le eclissi di Luna e la longitudine

Gli astronomi ellenistici (Ipparco e Tolomeo) e quelli medioevali potevano solo ricorrere alle eclissi di Luna per misurare la differenza di longitudine tra due luoghi. Quando si prevedeva che ci sarebbe stata un'eclisse di Luna, veniva organizzata un'osservazione congiunta del fenomeno nei due luoghi di cui si voleva misurare la longitudine. L'osservazione consisteva nel rilevare, con la maggiore precisione possibile, a che distanza dal mezzogiorno locale avveniva il fenomeno del contatto della Luna con l'ombra della Terra, misurando il tempo con orologi ad acqua, o aiutandosi con osservazioni astronomiche.

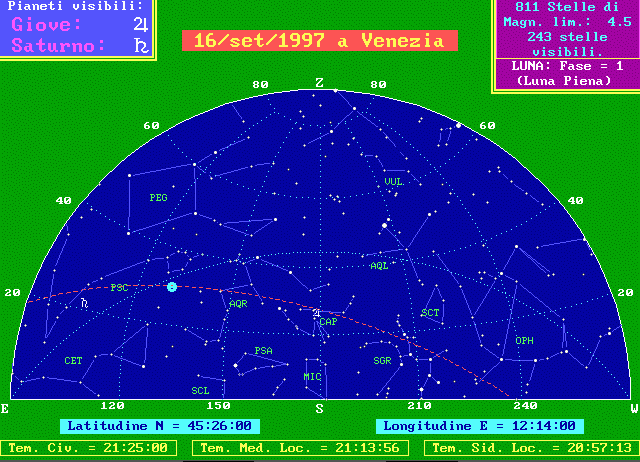
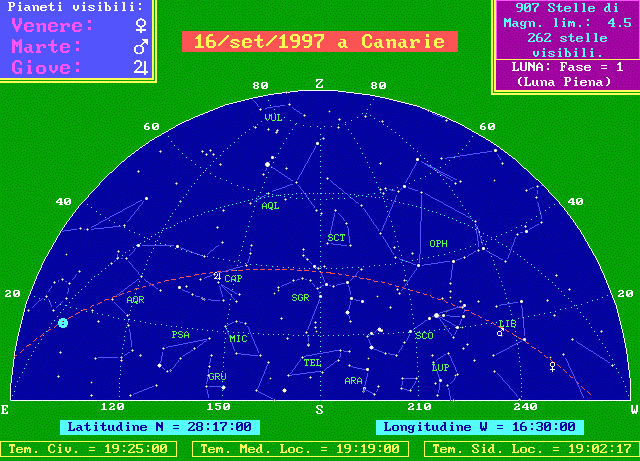
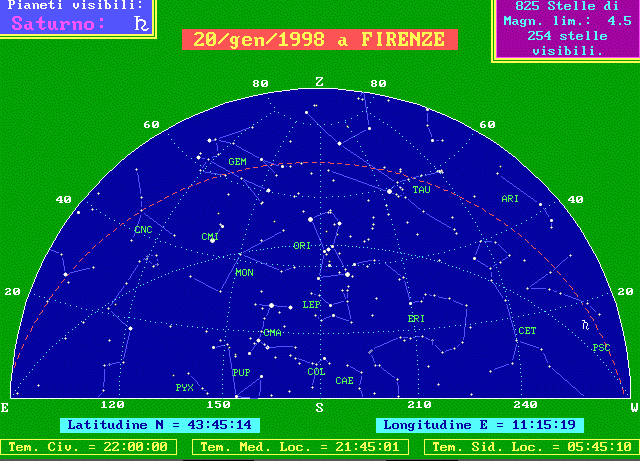
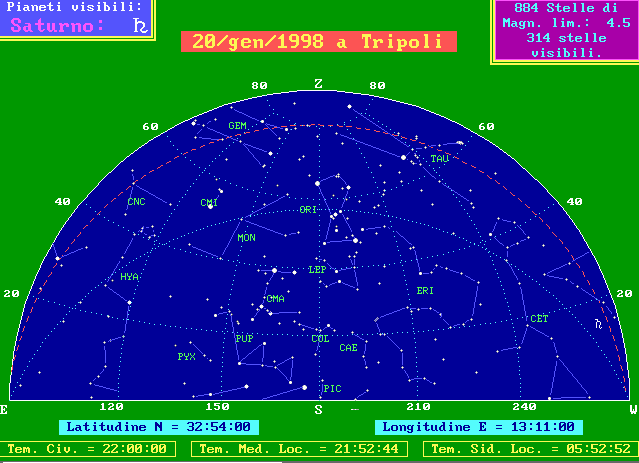
Alcune fasi dell'eclissi di Luna del 16 Settembre 1997 Dalla differenza tra i tempi locali (tempo solare o siderale) misurati nei due luoghi, si può ricavare la differenza di longitudine. Ovviamente nei due luoghi non solo è diverso il tempo, ma anche la posizione della Luna e di tutti gli altri corpi celesti, rispetto all'orizzonte ed al meridiano locali. Lo si può constatare nelle due cartine seguenti che rappresentano il cielo a Venezia ed alle Isole Fortunate (le Canarie), nel momento in cui la Luna emergeva dall'ombra della Terra il 16 Settembre 1997 (è stato scelto il momento dell'emersione, perchè all'immersione la Luna non era ancora sorta sull'orizzonte delle Canarie e perchè ci è piaciuto riferirsi ad un'eclissi totale e spettacolare che molti hanno potuto osservare). Per meglio leggere e comprendere queste cartine sono disponibili le istruzioni.

Il cielo a Venezia il 16/9/1997, alle ore 20:25 di tempo Universale.

Il cielo alle Isole Canarie il 16/9/1997, alle ore 20:25 di tempo Universale. Il ragionamento è il seguente: supponiamo che a Venezia la Luna si immerga nell'ombra della Terra alla mezzanotte, mentre nelle Isole Fortunate (Isole Canarie) lo stesso fenomeno avvenga alle dieci di sera, siccome il fenomeno in realtà è avvenuto nello stesso tempo, ma i due osservatori lo hanno visto ad una distanza apparente di due ore, questo significa che il Sole, per spostarsi dalla posizione dell mezzogiorno di Venezia a quella del mezzogiorno nelle isole Canarie impiega due ore. Ovvero, supponendo che il Sole se ne stia fermo in cielo (cosa che è vera solo in modo approssimativo), questo vuol dire che la Terra ci ha messo due ore per ruotare da Venezia alle isole Canarie rispetto ad un riferimento fisso, e quindi la differenza di longitudine è di 30 gradi, percorrendo la Terra quindici gradi all'ora nel suo moto di rotazione.

Ci si perdoni questo esempio che può sembrare strano, ma lo abbiamo parafrasato dalle dispense di un grande professore di Astronomia: Galileo Galilei.

Potete ottenere informazioni su le eclissi in rete: L'annuario di Arcetri alla sezione "eclissi" La pagina delle eclissi dell'Osservatorio di Catania L'Osservatorio Astronomico Torre Luciana con tante immagini e spiegazioni e che ci ha fornito l'immagine dell'eclissi di Luna

[Per tornare alla pagina precedente usare il bottone back del browser]

Il Sistema Equatoriale assoluto

Definiamo adesso un sistema di riferimento che sia svincolato dall'osservatore e solidale con la sfera celeste. In questo caso si prende come piano fondamentale il piano equatoriale, come cerchio origine quello generato intersecando la sfera con un piano passante per l'asse di rotazione del mondo e il punto equinoziale di Primavera o punto gamma. Non c'è alcun oggetto nel punto gamma, ma esso è facilmente individuabile perchè il Sole, la stella più splendente, si trova in esso all'equinozio di primavera. Il problema di sapere quando cade esattamente l'equinozio, fu risolto già dagli astronomi greci con semplici strumenti, come il cerchio di Ipparco.

Il cerchio giace nel piano dell'equatore celeste dove si trova il Sole nei giorni degli equinozi. In tutti i giorni dell'anno l'ombra del cerchio è un'elliisse, che diventa un segmento solo e soltanto il giorno degli equinozi.

Le coordinate di questo sistema sono l'ascensione retta (AR), di solito indicata anche con la lettera greca alfa, e la declinazione, indicata con la lettera greca delta; quest'ultima è definita nella stessa maniera in cui si definisce nel sistema equatoriale relativo.

L'ascensione retta di un astro è l'angolo diedro formato dai piani del cerchio origine e del cerchio massimo passante per l'astro e per i poli celesti. L'angolo viene contato da Ovest verso Est. In sostanza le coordinate, declinazione ed ascensione retta sulla sfera celeste, sono simili alle coordinate latitudine e longitudine sulla Terra, dove il ruolo del punto equinoziale di Primavera è quello dell'Osservatorio di Greenwich. Poichè le coordinate equatoriali sono completamente svincolate dal tempo e dalla posizione dell'osservatore, sono adatte per il confronto di osservazioni fatte in tempi e luoghi diversi e quindi per la costruzione degli atlanti e cataloghi stellari. In realtà le coordinate equatoriali variano lentamente nel tempo a causa della precessione degli equinozi.

A causa della rivoluzione della Terra, il Sole sembra percorrere la sfera celeste lungo un cammmino che lo riporta ad assumere la stessa posizione dopo un anno. Questo cerchio altro non è che il piano orbitale della Terra e poichè i piani orbitali dei pianeti sono poco inclinati rispetto ad esso, il cammino del Sole risulta essere una sorta di binario seguito da tutti i corpi mobili del cielo: Luna e pianeti. Gli antichi chiamarono questo binario Eclittica, luogo delle eclissi, perchè si accorsero che quando la Luna si trova esattamente su di esso può verificarsi un'eclissi.

Il punto Gamma permette di definire tre grandezze continuamente usate in Astronomia:

Tempo siderale locale (TSL). È l'angolo orario del punto Gamma che transita in meridiano ogni 23 ore e 56 minuti, il tempo di una rotazione terrestre. Tempo siderale, ascensione retta e angolo orario (HA) di un astro sono legati dalla relazione: TSL = AR + HA Anno siderale. È il tempo necessario affinchè il Sole si trovi, dopo aver interamente percorso l'eclittica, nella direzione della stessa stella.

Anno tropico. È il tempo necessario affinchè il Sole ritorni a congiungersi con il punto Gamma. A causa della precessione degli equinozi l'anno siderale è leggermete più lungo di quello tropico.

[Per tornare alla pagina precedente usare il bottone back del browser]

Il sistema di riferimento equatoriale relativo

In questo sistema si adotta come piano fondamentale il piano equatoriale, definito come il piano perpendicolare alla direzione dell'asse di rotazione terrestre. Il piano meridiano, come nel sistema alto-azimutale è il piano origine; le coordinate sono la declinazione, che spesso si individua con la lettera greca delta, e l' angolo orario, indicato con HA o con t. La declinazione è la distanza angolare tra la direzione dell'astro e il piano equatoriale, mentre l'angolo orario è l'angolo formato tra il piano verticale passante per i punti Nord e Sud dell'orizzonte (piano meridiano) e il piano contenente l'asse polare (NCP, SCP) e passante per l'astro. Nella consuetudine astronomica quest'angolo viene espresso in ore, minuti e secondi di tempo, intendendo che l'angolo di un'ora è l'angolo di cui è ruotata la Terra in un'ora, pari a 15°. Analogamente un minuto di tempo è equivalente a 15' e 1 secondo di tempo equivale a 15".

La figura mostra anche i rapporti geometrici tra le coordinate alto-azimutali e quelle equatoriali relative. Lo zenit (Z), il polo nord celeste (NCP) e la stella individuano un triangolo sferico i cui lati sono:

il complemento della latitudine, NCP-Z il complemento della declinazione, NCP-stella il complemento dell'altezza sull'orizzonte o distanza zenitale, Z-stella Gli angoli sono: l'azimut od il suo esplemento, NCP-Z-stella l'angolo orario, Z-NCP-stella l'angolo parallattico, Z-stella-NCP La risoluzione di questo triangolo corrisponde alla trasformazione delle coordinate alto-azimutali in equatoriali e viceversa, operazione che sta alla base della navigazione astronomica. Per questo motivo questo triangolo prende anche il nome di "triangolo nautico". In questo sistema una coordinata, la declinazione, non cambia al passare del tempo, mentre l'altra aumenta in modo proporzionale ad esso. Ciò non vale per tutti quei corpi che sono dotati di moto proprio rispetto alle stelle, come la Luna, il Sole, i pianeti, le comete ecc.

[Per tornare alla pagina precedente usare il bottone back del browser]

Equazione del Tempo e Tempo civile

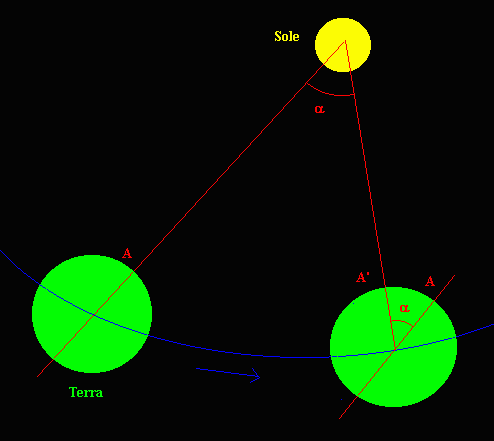
L'intervallo di tempo tra due culminazioni successive del Sole al meridiano dello stesso luogo (giorno solare vero) non è costante, ma varia di qualche secondo da un giorno all'altro.

Un osservatore in A vede nuovamente culminare il Sole, il giorno successivo, dopo che la Terra ha ruotato di un angolo di (360 + alfa)°. Mentre una rotazione completa della Terra si compie in 23 ore e 56 minuti ed è costante in durata, l'angolo alfa varia di giorno in giorno perchè l'orbita ellittica della rivoluzione terrestre viene percorsa con moto non uniforme. Pertanto, se si definisce il secondo come la 86.400 esima parte del giorno solare vero, avremo che l'unità di tempo in alcuni giorni è più corta ed in altri più lunga. Le esigenze della vita moderna impongono invece che l'unità di tempo sia rigorosamente costante e che la misura civile del tempo mantenga uno stretto rapporto con il Sole vero. Per realizzare ciò, alla fine del XVII secolo, è stato introdotto un artificio astronomico matematico: il Sole Medio.

Il Sole medio percorre l'equatore celeste con moto uniforme e quindi velocità angolare costante pari a (360/365.2422)° al giorno, nello stesso tempo in cui il Sole vero percorre l'intera eclittica nel suo moto apparente annuo. In questo modo il giorno solare medio dura 24 ore esatte. Tra Tempo solare vero (TSV) e tempo solare medio (TSM) vi è dunque una differenza, variabile di giorno in giorno, talvolta positiva, talvolta negativa, secondo che il Sole vero preceda o segua quello medio. Tale differrenza prende il nome di Equazione del tempo:

TSV - TSM = E

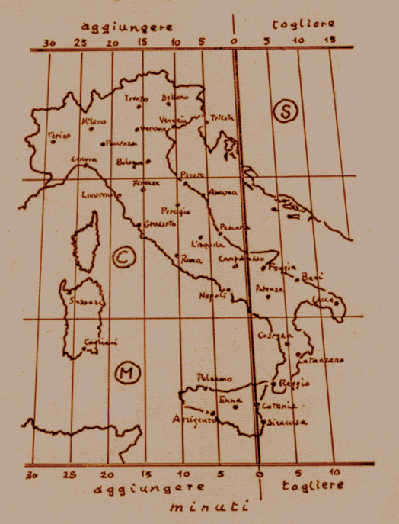
Nella figura viene tabulato il valore di E in minuti per i vari giorni dell'anno, raggruppati nei 12 mesi indicati con il numero cardinale arabo.

A causa della sfericità della Terra, il tempo solare medio è una quantità variabile con la posizione dell'osservatore. Per esempio, a S. Giovanni Valdarno che dista pochi chilometri da Firenze, il Sole vero o medio sorge, culmina e tramonta con circa un minuto di anticipo, mentre a Livorno con circa tre minuti di ritardo, sempre rispetto a Firenze. Con l'introduzione delle ferrovie e del telegrafo, già nel secolo scorso, ogni paese ha adottato il Tempo civile (TC) che è un tempo standard, convenzionalmente uguale per tutto un territorio, generalmente largo 15° in longitudine e detto fuso orario. Si definisce tempo civile di un fuso orario il tempo solare medio misurato lungo il meridiano centrale del fuso.

L'Italia si trova nel fuso orario dell'Europa centrale il cui meridiano centrale passa per Catania e si trova a circa 3° 45' ad Est di Firenze. Ne consegue che il Sole culmina a Firenze con circa 15 minuti di ritardo rispetto a Catania.

Indicando con DL la differenza di longitudine tra un luogo ed il meridiano centrale del fuso cui appartiene avremo:

TC = TSV - E + DL

[Per tornare alla pagina precedente usare il bottone back del browser]

Feaci

Inizialmente i Feaci dovevano essere delle divinità protettrici dei naviganti, che portavano in salvo i naufraghi. In seguito, secondo la leggenda, Poseidone, il dio del mare, irato perché i Feaci gli sottraevano troppi naufraghi, mise fine alla loro opera meritoria di salvataggio. Secondo Omero vivevano felici in una terra chiamata Scheria, sotto il regno di Alcinoo e la sua consorte Arete, rispettivamente padre e madre di Nausicaa, una delle più belle e delicate figure femminili della poesia greca.

[Per tornare alla pagina precedente usare il bottone back del browser]

Febbraio

Febbraio: è inverno nel villaggio di contadini, cè chi si scalda al fuoco, chi taglia la legna ....

[Per tornare alla pagina precedente usare il bottone back del browser]

Breve storia dei fusi orari

Nel passato ogni paese aveva un proprio tempo, fondato sul moto apparente del sole. Era misurato con il quadrante solare o la meridiana e quando il Sole passava per il meridiano locale era mezzogiorno. Purtroppo il Sole non è un orologio esatto per la mancanza di regolarità del suo moto apparente lungo l'eclittica e la durata del giorno, definita come l'intervallo tra due passaggi successivi del Sole al meridiano, è variabile. Queste differenze forse erano sfuggite agli antichi, che non avevano strumenti di misura precisi, ma erano ben conosciute dal 1657 in poi, con la scoperta dell'isocronismo delle oscillazioni del pendolo e la sua applicazione agli orologi. Gli orologiai di Parigi avevano adottato il motto: solis mendaces arguit horas per convincere i loro clienti della bontà dei loro orologi, che segnavano un tempo diverso da quello indicato dal Sole. Per ovviare a questo inconveniente fu introdotto un Sole fittizio, capace di muoversi regolarmente. In tale modo si può definire un giorno medio, costante tutto l'anno, e un tempo medio, diverso dal tempo vero. La differenza tra i due mezzogiorni (vero e medio) è compresa tra circa 16 minuti in più e 14 minuti in meno, valori estremi che sono raggiunti solo due volte l'anno; di solito la differenza è compresa entro i 5 minuti (circa 200 giorni) e in 4 giorni i due mezzogiorni coincidono.

La prima città ad usare il tempo medio fu Ginevra nel 1780 con il tocco della grossa campana del Duomo per annunziare il mezzogiorno, naturalmente medio. Londra introdusse il tempo medio nel 1792, Berlino nel 1810 e Parigi nel 1816. A Parigi il prefetto chiese un apposito rapporto al Bureau des Longitudes per rassicurare la popolazione, che temeva che il nuovo tempo potesse portare soprusi nel calcolo delle ore di lavoro (infatti, il mezzogiorno medio divideva in due parti diseguali l'intervallo fra il tramontare e il sorgere del Sole). In Italia il tempo medio fu adottato a Torino nel 1852, a Bologna nel gennaio 1858 e a Milano il 14 febbraio 1860. A Roma il tempo medio fu introdotto nel 1855 informalmente, ossia senza nessun decreto governativo, ma come conseguenza dello sviluppo delle ferrovie e del telegrafo. I conducenti delle vetture postali regolavano ogni mattino il loro orologio alla stazione di partenza, comunicavano poi l'ora al sagrestano e ai postini che la distribuivano alle case.

Tutti i paesi che sono situati su un medesimo meridiano contano, nello stesso istante, lo stesso tempo locale (medio o vero), ma, sempre nello stesso istante, il tempo locale è differente da paese a paese, quando questi non si trovano sullo stesso meridiano. I loro tempi locali differiscono di una quantità costante che è uguale alla differenza di longitudine tra i due luoghi (per ogni grado di longitudine verso ovest il mezzogiorno locale capita quattro minuti più tardi). In genere non si ha idea del modo rapido con cui variano i tempi locali al variare della longitudine; ad esempio, alla nostra latitudine, la variazione del tempo locale è già di un minuto per soli 20 chilometri di distanza in senso est-ovest.

La discordanza dei tempi locali, mentre non era notata nell'ambito della comunità locale, cominciò a creare problemi quando le persone iniziarono a spostarsi facilmente tra città e province diverse, cosa resa possibile dallo sviluppo delle ferrovie. Una volta, solo con viaggi della durata di parecchi giorni, si poteva percorrere una differenza di longitudine di un'ora e nelle relazioni commerciali non si badava ad un'incertezza, nella determinazione del tempo, anche di una frazione d'ora. Le ferrovie (e il telegrafo) imponevano, invece, di tenere conto dei minuti e delle loro frazioni.

Era necessario ripensare il sistema del tempo, soprattutto per le ferrovie che dovevano funzionare con regolarità e sicurezza. All'inizio, infatti, non esistevano che tronchi isolati e l'ora che regolava la loro attività era quella della città principale da cui partiva il tronco. Diventando però la struttura ferroviaria più complessa, si formarono tante ore ferroviarie quante erano le città principali e nelle stazioni di passaggio da un tronco all'altro si passava dal regime di un'ora a quello di un'altra.

Riprendendo un'idea formulata nel 1828 dall'astronomo John Herschel, venne proposta un'unificazione regionale o anche nazionale delle diverse ore ferroviarie, cioè un'ora ferroviaria unica (generalmente quella della capitale o di una città opportuna). Quest'unificazione venne attuata per la prima volta nel 1848 in Gran Bretagna (ora di Greenwich per l'Inghilterra e la Scozia, e ora di Dublino per l'Irlanda) e tale ora venne estesa anche alla vita pubblica. Era comune in Inghilterra, anche all'inizio del secolo XX, quando si parlava del tempo di Greenwich, chiamarlo tempo ferroviario. In Italia, nel 1866, erano sei le ore ferroviarie (Torino, Verona, Firenze, Roma, Napoli, Palermo). In quell'anno fu deciso di unificarle adottando il tempo medio di Roma (anche se non faceva parte del Regno). Il 12 dicembre 1866, coll'attivazione dell'orario invernale, esso venne introdotto nelle ferrovie, poste e telegrafi, non solo nel servizio interno, ma anche nei rapporti col pubblico. Inoltre, non per legge, ma per libera iniziativa delle principali città italiane, con motivazioni legate ai vantaggi pratici derivanti dalla concordanza dell'ora ferroviaria con quella cittadina e anche per motivi patriottici, venne deciso di estendere l'ora di Roma alla vita pubblica e privata, diventando in sostanza un'ora nazionale. Milano regolò gli orologi pubblici sul tempo di Roma lo stesso 12 dicembre 1866, Torino e Bologna il 1 gennaio 1867, Venezia il 1 maggio 1880 e ultima Cagliari nel 1886. L'ora nazionale era stata precedentemente adottata dalla Gran Bretagna, come abbiamo visto, e venne adottata dalla Svezia nel 1879, che fece una scelta rivoluzionaria adottando non l'ora di Stoccolma, ma quella del meridiano di Greenwich. La Francia introdusse l'ora nazionale unicamente dal 14 marzo 1891, usando il tempo di Parigi. Una piccola curiosità: nella stazioni ferroviarie francesi gli orologi esterni erano regolati sul tempo di Parigi, mentre quelli interni erano in ritardo di 5 minuti; questo per fare fretta ai viaggiatori.

Se il passaggio dal tempo locale all'ora ferroviaria e poi all'ora nazionale permetteva di raggiungere una un'uniformità di misura del tempo all'interno d'ogni Stato, rimaneva il grosso problema della diversità d'ora quando si passava il confine. Guardando un vecchio orario ferroviario, c'era per l'Italia una differenza di 47 minuti con l'ora ferroviaria francese, di 20 minuti con quella svizzera, e di 10 con l'ora ferroviaria austro-ungarica. Per i lunghi viaggi le cose si complicavano, essendo necessario passare attraverso più stati: da Roma a Pietroburgo c'erano 7 diverse ore e ben 12 da Parigi a Costantinopoli, senza contare le ore prussiane, numerose quanto le stazioni (con il sistema prussiano gli orari ferroviari per il pubblico erano compilati sulle ore locali, mentre per il personale del treno, che non poteva regolarsi su ore variabili da luogo a luogo, erano disponibili appositi orari di servizio, redatti sulla base di un'ora unica, ossia un'ora ferroviaria interna. Il personale doveva servirsi di due misure diverse di tempo, a seconda che rispondeva al pubblico o al servizio interno).

Si ripeteva, insomma, in campo internazionale, il medesimo inconveniente che si era verificato nei rapporti fra le varie città quando vigevano le ore locali; come queste avevano ceduto il posto alle ore ferroviarie e nazionali, ci si chiedeva se queste a loro volta non dovessero essere abbandonate per raggiungere un'unificazione mondiale.

La soluzione non era banale: dovevano essere sacrificate le ore nazionali e questo poteva creare problemi politici, ma si doveva anche arrivare all'unificazione senza grandi riforme radicali, perché la vita era regolata dal Sole e non dovevano essere imposte ore troppo diverse da quelle reali. La riforma radicale possibile era l'ora universale assoluta, proposta da Theodor von Oppolzer (1841-1886, direttore dell'Osservatorio Astronomico di Vienna) che estendeva semplicemente a tutto il globo e per tutti gli usi l'ora di Greenwich o quella di un altro meridiano di riferimento. In tutto il mondo gli orologi avrebbero segnato la stessa ora. Il giorno legale sarebbe cominciato su tutto il globo alla mezzanotte di Greenwich, quando però a New York erano le sette di sera, a Pechino le otto di mattina, ecc. quindi le parole oggi, ieri, domani, avrebbero perso ogni significato e si sarebbe andati incontro alla più grande confusione. Per esempio, con il tempo universale noi potremmo leggere di un americano della costa Est che si alza alle 11, tempo universale, e pensarlo un dormiglione. Se invece ci ricordiamo che l'ora di Washington è in ritardo di cinque ore su quella di Greenwich, ecco allora che il nostro amico americano si sveglia alle 6 tempo locale, e non è affatto un dormiglione.

Quirico Filopanti (pseudonimo di Giuseppe Barilli, 1812-1894), professore e politico bolognese, già nel 1859 suggeriva, nel suo libro Miranda (scritto durante l'esilio inglese), una geniale soluzione. Proponeva di dividere la terra per mezzo dei meridiani in 24 zone longitudinali, o fusi, che differivano l'uno dall'altro di un'ora, coincidendo nei minuti e nei secondi. Il primo fuso era centrato sul meridiano di Roma e comprendeva l'Italia, la Germania, la Svezia e parte dell'Africa. Se in questo erano le sei del mattino, nel secondo fuso procedendo verso Occidente sarebbero state le sette e cosi via. Filopanti introduceva inoltre un tempo universale da usarsi nell'astronomia e nei telegrafi. Per dare ai cittadini la conoscenza del tempo universale e del tempo locale gli orologi avrebbero avuto due sfere: una portante una lettera U per il tempo universale, l'altra con una lettera L per il tempo locale; la sfera dei minuti serviva per entrambi i tempi. Filopanti concludeva scrivendo che "quando un orologio ben regolato a tempo medio, universale o locale, batterà un'ora qualunque, tutti gli orologi del mondo suoneranno in quel medesimo instante, e indicheranno o quella stessa ora, od una qualunque altra ora intera".

La proposta di Filopanti era molto pratica, anche se la sua inspirazione era etico-religiosa. Essendo la terra divisa nel senso della longitudine in 360 gradi, dividendo la superficie del globo in 24 zone, ogni zona viene ad essere limitata da due meridiani discosti di 15 gradi, a ognuna corrisponde l'ora del suo meridiano medio, discosto di sette gradi e mezzo dai due estremi. Con il sistema dei fusi orari si raggiunge la desiderata unificazione nella misura del tempo. Infatti, gli Stati compresi nello stesso fuso vengono ad avere la stessa ora, la differenza tra due fusi limitrofi è di un,ora precisa e le diverse ore sono facilmente paragonabili tra loro. Infine, si raggiunge l'unificazione del tempo senza discostarsi troppo dall'ora reale, perché la differenza fra l'ora normale e quella locale non supera mai la mezz'ora, adottando ogni Stato l'ora del fuso entro cui giace il suo territorio o la sua massima parte.

Perché allora quando si parla di fusi orari Filopanti viene raramente ricordato? Probabilmente perché la sua proposta era in anticipo (ricordiamoci che nel 1859 unicamente la Gran Bretagna aveva l'ora nazionale e la maggiore parte degli altri Stati era ancora regolata dalle ore locali) oppure non era nello spirito del tempo (nel 1872 il dibattito era sull'ora universale assoluta, dibattito che continuerà sino alla fine del secolo). Soprattutto, però, non c'era nessuna struttura economica forte disposta a sostenerla, come potevano essere le grandi compagnie ferroviarie o telegrafiche, le più interessate a stabilire un sistema per regolare il tempo.

Per capirlo trasferiamoci negli Stati Uniti d'America. Date le grandi dimensioni (in senso longitudinale) della nazione non era possibile un solo tempo ferroviario o nazionale; di conseguenza ogni compagnia ferroviaria aveva sviluppato un proprio orario. All'inizio del 1870 se ne contavano circa 50 e ogni città aveva un proprio tempo locale e tanti tempi ferroviari quante erano le linee che la servivano. Per esempio, nella stazione di Pittsburgh c'erano cinque orologi che indicavano i diversi tempi delle ferrovie e il tempo locale.

Charles F. Dowd (1825-1904), rettore di un collegio femminile a Saratoga Springs, NY, propose nel 1870 un System of National Time for Railroads fondato sulla longitudine. Il tempo di Washington sarebbe stato il tempo standard, lo Standard Time, e per omologare l'ora ferroviaria con l'ora locale, ad ogni multiplo di quindici gradi da Washington (che corrisponde ad un'ora, come abbiamo visto) si sarebbe tolta un'ora, dividendo gli Stati Uniti in quattro zone. Dowd presentò prima la sua idea ad una convenzione di sovrintendenti ferroviarie e poi in un opuscolo. L'opuscolo, che conteneva una descrizione dei principi scientifici su cui si basava la proposta e un esempio di orario per tutte le linee ferroviarie, ebbe un'ampia diffusione. Venne discussa unicamente l'opportunità dell'uso del meridiano di Washington che Dowd sostituì con il meridiano di Greenwich, già usato dagli Stati Uniti in campo marittimo (dal 1850). Sulla tomba di Dowd si trova una lapide di bronzo che riporta tra l'altro l'inscrizione: In solving the problem of standard time he proved himself a world benefactor. Incredibilmente, il contributo di Dowd alla definizione dello Standard Time è poco conosciuto non soltanto in Europa, ma anche negli Stati Uniti.

Contemporaneo di Dowd fu Sir Sandford Fleming (1827 – 1915), ingegnere capo delle ferrovie canadesi, che, generalmente, viene considerato l'inventore dei fusi orari. Non si hanno notizie di un suo interesse sul problema del tempo, prima del 1876 quando apparve una memoria chiamata Terrestrial Time, stampata privatamente, che venne poi riscritta, ampliata e pubblicata nel 1878. La memoria proponeva che gli orologi di tutto il mondo allo stesso momento indicassero la stessa ora, che Fleming suggeriva di chiamare Uniform Time o Terrestrial Time. In tale modo, se il suo sistema fosse stato adottato, si sarebbe usato il tempo locale per la vita di tutti i giorni, mentre, quando fosse stato necessario avere un'ora esatta sarebbe stato usato il Terrestrial Time. Un uso, anche se codificato per legge, che avrebbe creato grande confusione: basti pensare, ad esempio, agli stati distanti dal meridiano iniziale. Anch'egli proponeva un orologio con un doppio sistema di lancette per indicare i due tempi.

L'adesione al sistema dei fusi orari venne nel 1879, quando in una conferenza si propose l'estensione del sistema di Dowd al mondo intero. Fleming, che proponeva la creazione di 24 Standard Time che avrebbero dovuto sostituire il tempo locale in ogni zona e che avrebbero differito per multipli interi dal meridiano iniziale, ebbe parte importante nella preparazione della International Meridian Conference convocata nell'agosto del 1884 a Washington dal Presidente Chester A. Arthur per discutere della scelta di un meridiano iniziale (longitudine zero) e della creazione di un'ora internazionale per regolare l'amministrazione delle ferrovie, dei telegrafi e delle poste La stessa questione era già stata discussa alla conferenza geodetica di Roma del 1883, ma senza accordi. La ragione di questa unificazione era prettamente scientifica, producendo la mancanza di un'ora unica "perditempi incresciosi sentiti da color che in questioni di astronomia, di geografia fisica, di geologia, sono portati ad estendere le proprie ricerche a luoghi della terra disparati e lontani". Nelle risoluzioni finali venne scritto che " il congresso propone di adottare come primo meridiano quello che passa per il centro dello strumento dei passaggi dell'osservatorio di Greenwich il congresso propone inoltre l'adozione di un giorno universale, il quale venga usato in quei casi in cui si crederà utile, senza per questo proporre l'eliminazione dei tempi locali e di altri tempi ora in uso".

Giovanni Celoria, allora secondo astronomo dell'Osservatorio di Brera, commentando le decisioni del congresso scriveva che " dal punto di vista pratico e della vita civile l'ora universale ha un valore minimo. Sarebbe grottesco, per non dire peggio, che gli abitanti di San Francisco, ad esempio, dovessero contare mezzogiorno verso le quattro del mattino del loro tempo locale. Evidentemente gli affari e la vita degli abitanti di una data regione non possono regolarsi su altro tempo che sul locale, o al più su un tempo che dal locale di poco differisca ed abbia col tempo universale un rapporto assai semplice. Gli Stati Uniti hanno risolto il problema felicemente. Il paese fu quindi diviso in quattro sezioni, governate rispettivamente dal tempo dei meridiani che passano a 75, 90,105 e 120 gradi ovest dal meridiano di Greenwich…tutti differiscono dall'ora universale di un numero intero di ore per passare negli orari delle ferrovie e dei telegrafi da uno ad altro tempo basta cambiare l'ora, mantenere invariati i minuti e questo calcolo semplice e spedito non ammette errori e confusioni. In Europa le diverse nazioni, essendo in generale i loro territori poco estesi in longitudine, regolano adesso gli orari su tempo di uno fra meridiani nazionali. La sola riforma che dal punto di vista internazionale sarebbe utile sarebbe di scegliere come nazionali tempi che differissero fra loro e dal tempo universale di una parte aliquota o di un numero intero d'ore, rendendo in tale modo facile e spedito il passaggio dall'uno all'altro. Ma a questa riforma e al tempo universale nella più gran parte di Europa per ora non si pensa."

Filopanti era arrivato agli stessi concetti 25 anni prima!

Comunque negli Stati Uniti e in Canada lo Standard Time entrò in vigore su iniziativa dell'American Railway Association a mezzogiorno del 18 novembre 1883 e rapidamente venne esteso a tutti gli usi civili. La molteplicità degli orari ferroviari e l'impraticabilità del tempo universale assoluto per scopi pratici era stata determinante. Fondamentale, per la sua introduzione, fu anche W.F.Allen, segretario della General Time Convention, che era l'organizzazione preposta all'orario e alla sicurezza delle linee ferroviarie: egli mostrò come l'idea dello Standard Time corrispondeva alle esigenze delle linee ferroviarie (infatti, il numero delle ore ferroviarie si ridusse da 56 a quattro).

Le opposizioni non furono molte: alcuni affermarono che il tempo locale era il tempo di Dio, altri si lamentarono della zona in cui erano stati inseriti e continuarono a usare il vecchio sistema orario. A New York in quel giorno vennero suonati due mezzogiorni, uno con il tempo locale e l'altro con lo Standard Time.

L'estensione dei fusi orari al mondo non fu immediata. Sostanzialmente le perplessità erano legate alla paura di perdere l'ora nazionale, di rendere facile la confusione delle ore dei vari fusi e di non avere delle linee ben definite di confine dei fusi, ma il vantaggio pratico che presentavano, e che li faceva preferire all'ora universale, fu determinate.

In Europa deciso sostenitore del nuovo sistema fu il tedesco Ernst von Hesse-Wartegg con il suo libro Die Einhetszeit nach Stundenzonen . Decisivo fu però lo schierarsi del maresciallo Moltke che nel 1891 ne invocò l'adozione da parte della Germania; forte era la paura che l'anarchia delle ore ferroviarie potesse essere causa di eventuali incagli e ritardi nella mobilitazione dell'esercito tedesco.

In Italia il sistema venne adottato il 10 agosto 1893 con regio decreto (il meridiano che dà il tempo al fuso nel quale sta l'Italia, e che è il secondo, passa per l'Etna). Nella notte del 31 ottobre gli orologi delle amministrazioni ferroviarie e governative furono mandati avanti di 10 minuti, essendo questa la differenza fra il tempo di Roma e quello dell'Europa Centrale e cosi il nostro paese realizzò "nella sua migliore parte, quella trasformazione dell'ora che un italiano di molto ingegno Q. Filopanti immaginava primo fra tutti , fin dal 1859".

Nel 1897 praticamente tutti i paesi europei avevano adottato il sistema delle zone orarie con la sola eccezione della Francia. Questo paese, solo con una legge del 1911, adottò il tempo di Greenwich, dichiarando però che si trattava del tempo di Parigi ritardato di 9 minuti e 21 secondi.

---

• Questo scritto è stato tratto da: Quirico Filopanti: una singolare figura di astronomo nella Bologna dell'Ottocento, presentato dagli autori, Gianluigi Parmeggiani e Fabrizio Bònoli (Osservatorio Astronomico di Bologna e Dipartimento di Astronomia dell'Università di Bologna) al Seventh Annual Meeting on the History of Astronomy: Astronomical Observatories and Institutes in Italy, tenutosi a Milano il 21-22 aprile 1995 e pubblicato in Memorie della Società Astronomica Italiana, vol. 66, N. 4, pagg. 861-870, 1995

[Per tornare alla pagina precedente usare il bottone back del browser]

L'orologio H1

Ci sono dei documenti che fanno pensare che John Harrison iniziò la costruzione del suo primo cronometro marino, conosciuto comunemente come "H1", intorno al 1729. I disegni, che sono del 1727, si concludono con una presentazione dello strumento in cui il loro autore prevedeva che l'orologio, a bordo di una nave, avrebbe potuto funzionare con un errore massimo di 3 o 4 secondi al mese. Forse questa affermazione, troppo ottimistica, fu dettata dalla necessità di trovare un finanziatore per la sua costruzione ed in effetti, convinse un provetto costruttore di orologi come Graham che concesse ad Harrison un prestito senza interessi, da restituirsi quando poteva. A maggior onore di Graham va il fatto che Harrison era un suo potenziale concorrente, nel costruire un cronometro marino affidabile.

L'orologio H1. L'esemplare, alto 63 cm. e del peso di circa 40 chili, è conservato presso il National Maritime Museum di Greenwich Il primo grande progresso nella meccanica di H1 è costituito dal dispositivo che mantiene costante la coppia motrice della molla, nel momento in cui si carica l'orologio. Il sistema esisteva già, ma non poteva essere utilizzato a bordo di una nave, perche si basava su dei pesi e in genere non funzionava bene, mentre quello di Harrison si rivelò molto affidabile. Un ulteriore dispositivo, che di per se stesso rappresenta un grande progresso tecnologico, è costituito dall'introduzione di cuscinetti a rulli per minimizzare gli attriti. Gli assi, difatti, non si muovono dentro fori ricavati nelle pareti portanti, ma bensì rotolano su piccoli rulli di appoggio.

Tuttavia il grande progresso di H1, rispetto gli orologi esistenti è costituito dal nuovo sistema di regolatore adottato. Ogni orologio per funzionare ha bisogno di un fenomeno periodico che ne regoli il movimento. Da Galileo, ma forse sarebbe meglio dire da Huygens in poi, l'oscillazione è quella di un pendolo che, muovendo un'ancorina, fa ruotare di un angolo prefissato un ingranaggio che, a sua volta, dà al pendolo una piccola spinta, per evitare che l'attrito meccanico e la resistenza dell'aria ne esauriscano l'energia. Il pendolo su una nave non è utilizzabile a causa del rollio e del beccheggio e quindi Harrison lo sostituì, con successo, con due barre accoppiate da molle. Queste, oscillando attorno al proprio asse di rotazione, facevano benissimo la funzione del pendolo, senza risentire dei movimenti della nave. Le barre, infatti, sono indipendenti dal moto della nave perché non utilizzano, come forza di richiamo, la gravità, come accade nel pendolo, ma bensì la forza elastica delle molle. Nel sistema a barre, però, il periodo di oscillazione dipende dalla temperatura dell'ambiente in cui si trova l'orologio. Un allungamento delle barre con il riscaldamento comporta l'aumento del periodo di oscillazione e quindi un rallentamento dell'orologio. Per eliminare questo fenomeno Harrison decise di intervenire sulla posizione delle molle di richiamo, costruendo un dispositivo che, dilatandosi, spostava l'appoggio delle molle, per cui gli effetti della dilatazione delle barre oscillanti venivano praticamente compensati dalla variazione della forza elastica delle molle stesse. H1, con la sua precisione e la sua stabilità, soddisfece il suo costruttore, ma aveva caratteristiche intrinseche che ne impedivano la produzione in serie ed era, inoltre, molto ingombrante e non poteva essere facilmente trasportato, se non per nave. Per questo motivo Harrison chiese ed ottenne dal Board of Longitudes un finanziamento per costruirne una versione più piccola e più leggera.

[Per tornare alla pagina precedente usare il bottone back del browser]

L'orologio H2

Harrison decise di fare il suo secondo cronometro marino, quello che si chiamerà "H2", più stretto e più alto rispetto ad H1. L'orologio doveva poter stare nella cabina del capitano, senza costringerlo a dormire sul ponte. Tuttavia "H2" risultò più pesante di "H1", 39 kg contro 34. La differenza è dovuta al fatto che "H1" aveva alcuni ingranaggi in legno, materiale che fu abbandonato nella costruzione di "H2". Al peso di "H2" va aggiunto quello della sospensione cardanica che aveva il compito di ridurre l'effetto delle oscillazioni della nave sull'orologio. La sospensione che è andata persa, si dice, pesasse all'incirca 28 kg. Dal punto di vista meccanico "H2" è uno sviluppo di "H1", con alcune aggiunte significative come, per esempio, una seconda molla motrice per mantenere costante la coppia al momento della ricarica e un dispositivo che evitava la sovraccarica.

Il secondo cronometro marino costruito da Harrison. Il cronometro che è alto 66 cm. si trova al National Maritime Museum di Greenwich "H2" fu completato nel 1739 e durante i due anni successivi fu confrontato con "H1". In seguito, quando il nuovo orologio fu presentato alla Royal Society, sappiamo che fu agitato, fu sottoposto a sbalzi di temperatura, insomma a tutte quelle situazioni ambientali che avrebbe potuto trovare in mare. Il risultato di tutte queste prove preliminari sembrava indicare che l'orologio sarebbe stato capace di assicurarsi il massimo premio messo in palio dal Board of Longitudes. John Harrison aveva 46 anni quando finì l'orologio "H2" e, di sua iniziativa, dette inizio alla costruzione di un terzo orologio, quello che si chiamerà H3. La ragione la troviamo nelle parole dello stesso Harrison: non è utile andare in mare per provarlo, perché una macchina molto migliore è, in gran parte, già costruita. Ma, diciamo noi, "H3" non era poi così dietro l'angolo: ci vorranno circa altri venti anni, perché questo il terzo orologio della serie venga completato.

[Per tornare alla pagina precedente usare il bottone back del browser]

L'orologio H3

John Harrison aveva promesso al Board of Longitudes di produrre il terzo orologio, detto "H3", entro il primo di Agosto del 1743. Purtroppo non poté mantenere la parola data, poichè il progetto conteneva degli errori. Nel cercare di risolvere questo problema, Harrison riuscì a trovare soluzioni tecniche che poi resero possibile la costruzione dell'ultimo orologio, l'H4. Harrison considerava inaffidabili le barre oscillanti, che avevano preso il posto del pendolo, quando l'orologio veniva sottoposto a rotazioni, come accade ad una nave durante una tempesta e le sostituì con una sorta di ruota oscillante accoppiata ad una molla a spirale. Questo meccanismo, adesso, non desta meraviglia, perché è utilizzato in tutti gli orologi meccanici, ma per allora era una novità assoluta. "H3" inoltre ha i cuscinetti a sfere (o meglio a rulli), il che abbassa ulteriormente l'attrito degli ingranaggi. Risolse anche altri due problemi fondamentali, il primo consisteva nel fatto che la molla di torsione che riporta in posizione la ruota oscillante non si comportava come la gravità con il pendolo, e il secondo riguardava la compensazione degli effetti delle variazioni di temperatura.

Il terzo cronometro marino costruito da Harrison. Il cronometro che è alto 59 cm., si trova al National Maritime Museum di Greenwich Comunque, dopo tante fatiche e, supponiamo, lunghe prove per verificarne la precisione, Harrison dichiarò pronto l'"H3", il 28 Novembre 1757. Per tutto il periodo impiegato a costruire "H3", ricevette dallo Stato circa 112 sterline l'anno, meno di quanto guadagnava un esattore delle tasse.. Per questa modica cifra l'Inghilterra si era assicurata uno dei più grandi risultati della ricerca tecnologica del XVIII secolo, e il mondo si era arricchito di invenzioni che avrebbero permesso, in futuro, di migliorare le macchine e di inventarne di nuove, come appunto il cuscinetto a sfere.

[Per tornare alla pagina precedente usare il bottone back del browser]

L'orologio H4

John Harrison, troppo impegnato a costruire un orologio capace di vincere il premio messo in palio dal Board of Longitudes, aveva bisogno di un orologio per se stesso e se lo fece costruire da un certo John Jefferyes, orologiaio. Confrontato con un qualsiasi orologio da tasca del tempo, questo nuovo orologio presentava delle soluzioni innovative che, chiaramente, dovevano essere state suggerite da Harrison stesso al Jeffreys. Harrison ci ha lasciato scritto che l'orologio funzionava piuttosto bene e, pignolo come era, dobbiamo credere che fosse davvero eccellente anche se non adatto per andare in mare, perché privo di compensazione per le variazioni di temperatura. Pensiamo che Harrison, verificandone il funzionamento, deve avere intuito che sarebbe stato possibile renderlo tanto preciso da poterlo utilizzare per la navigazione.

Nel 1755, il 19 Giugno, Harrison ottenne dal Board of Longitudes una ulteriore assegnazione di 500 sterline per completare H3 e costruire due orologi da tasca, il più perfetti possibile. Dei due che doveva costruire, Harrison ne costruì uno solo che prese il nome di "H4". Questo orologio non era proprio un orologio da tasca, aveva infatti un diametro di circa 13 cm., ma era sufficientemente maneggevole e forse, nelle intenzioni di Harrison, doveva servire come orologio secondario per trasportare il tempo dall'orologio H3, nella cabina del capitano, sul ponte della nave, dove venivano eseguite le osservazioni astronomiche per determinare la longitudine. Il tempo impiegato da Harrison per costruire H4 è breve rispetto a quello speso per costruire H3, evidentemente già il suo orologio da tasca, a cui abbiamo accennato, doveva essere stato un buon banco di prova per la miniaturizzazione delle soluzioni meccaniche adottate per "H3".

L'orologio H4 costruito da John Harrison che ha vinto il premio del Board of Longitudes. Il diametro della cassa è di 13.3 cm. L'orologio è attualmente conservato presso il National Maritime Museum of Greenwich. Sappiamo che l'orologio H4, il 18 Luglio del 1760, non era completo perché la compensazione della temperatura ancora non funzionava al meglio, ma nell'anno successivo l'orologio fu pronto per il collaudo e in Febbraio Harrison chiese ufficialmente che, sia l'orologio "H3", che l'orologio "H4", fossero provati in mare, come richiedeva il bando di concorso. Harrison credeva di essere giunto alla felice conclusione della sua vicenda, ma non aveva fatto i conti con un potente astronomo molto invidioso.

[Per tornare alla pagina precedente usare il bottone back del browser]

AL-IDRISI

Abu Abdallah Muhammad Ibn Muhammad Ibn AbdallahIbn Idris al-Qurtubi al-Hasani nacque a Ceuta, in Spagna nel 1099 a.C. Fu educato a Cordoba e, dopo un lungo periodo di viaggi, si stabilì alla corte normanna di Palermo. La data della sua morte è controversa, potrebbe essere tanto il 1166 quanto il 1180. Le circostanze che lo portarono al servizio del re normanno Ruggero II non sono affatto chiare, i biografi arabi lo considerarono un rinnegato. Il suo contributo principale alla scienza fu nel campo della botanica, con particolare riferimento alle piante medicinali. Anche nella geografia il suo contributo fu però interessante, sappiamo che costruì per il suo sovrano un planisfero in argento e descrisse le terre conosciute in un libro intitolato "il libro di Ruggero" che, in sostanza, è un'enciclopedia geografica in cui si possono trovare informazioni sull'Asia, sull'Africa e sulle terre occidentali. Dopo il successo di questo libro, al-Idrisi volle ampliarlo e lo ripubblicò col titolo "Piacere degli uomini e diletto delle anime". I suoi libri di geografia furono molto letti, in versione latina, nei secoli successivi per la loro chiarezza e la loro semplicità.

[Per tornare alla pagina precedente usare il bottone back del browser]

Gennaio

Gennaio: il mese in cui si fanno i regali.

[Per tornare alla pagina precedente usare il bottone back del browser]

Luglio

Luglio: si miete il grano e si taglia la lana alle pecore.

[Per tornare alla pagina precedente usare il bottone back del browser]

Giugno

Giugno: tutti insieme i contadini tagliano e raccolgono il fieno. In questo mese inizia l'estate, controllate la data...

[Per tornare alla pagina precedente usare il bottone back del browser]

Lamo

Città che si trova nelle zone settentrionali della Terra. Infatti Omero ci indica che in quelle terre un pastore insonne, potrebbe ottenere due paghe, una per il giorno e un'altra per la notte che è luminosa.

[Per tornare alla pagina precedente usare il bottone back del browser]

LEAP SECOND ALERT!

---

                    U.S. NAVAL OBSERVATORY
                 WASHINGTON, D.C.  20392-5420
                               
                                            July 23, 1998
                                            No. 64

              TIME SERVICE ANNOUNCEMENT SERIES 14
                               
                         UTC TIME STEP

1. The International Earth Rotation Service (IERS) has announced the introduction of a time step to occur at the end of December, 1998.

2. Coordinated Universal Time (UTC) will be retarded by 1.0s so that the sequence of dates of the UTC markers will be:

              1998 December 31   23h   59m   59s
              1998 December 31   23h   59m   60s
              1999 January  01    0h    0m    0s

3. The difference between UTC and International Atomic Time (TAI) is:

from 1997 01 Jul, UTC to 1999 01 January, UTC: TAI-UTC= +31s from 1999 01 Jan, UTC until further notice: TAI-UTC= +32s

4. The insertion of one leap second will be evident by the change of sign of the DUT1 correction which will become positive. Extrapolated values of DUT1 are distributed weekly in the IERS Bulletin A.

5. All coordinated time scales will be affected by this adjustment. However, Loran-C and GPS will not be adjusted physically. Times of Coincidence for LORAN-C are available on the Time Service Web Page (http://tycho.usno.navy.mil/loran.html). For GPS, the leap second correction contained within the UTC data of subframe 4, page 18 of the navigation message transmitted by satellites will change.

    Before the leap second
    GPS-UTC = +12 (i.e., GPS is ahead of UTC by twelve seconds)

    After the leap second
    GPS-UTC = +13s (i.e., GPS will be ahead by thirteen seconds)

                             DENNIS D. McCARTHY
                             Director
                             Directorate of Time

Time Service Dept., U.S. Naval Observatory, Washington, DC

[Per tornare alla pagina precedente usare il bottone back del browser]

Le coordinate geografiche

Avvolgiamo la Terra in un reticolato di circoli Paralleli all'Equatore e di circoli Meridiani, convergenti nei Poli. Possiamo infittire il reticolato a piacere, perciò ogni punto si trova all'intersezione di un parallelo con un meridiano e ad esso corrisponde una coppia di numeri: le sue coordinate geografiche, la latitudine e la longitudine.

Latitudine

Si definisce latitudine di un luogo della Terra, l'angolo compreso tra il raggio terrestre che passa per quel luogo e il piano dell'Equatore. Tutti i luoghi che hanno la stessa latitudine stanno sullo stesso parallelo.

Longitudine

Si definisce longitudine di un luogo l'angolo diedro compreso tra il piano del meridiano di riferimento ed il piano del meridiano del luogo. Storicamente sono stati assunti quali meridiani di riferimento i meridiani passanti per vari luoghi. Da circa 200 anni il meridiano di riferimento per tutti gli abitanti della Terra è quello passante per l'Osservatorio di Greenwich in Inghilterra. Tutti i luoghi che si trovano sullo stesso meridiano hanno la stessa longitudine.

[Per tornare alla pagina precedente usare il bottone back del browser] [indice]

Il cielo è diverso se osservato da luoghi diversi della Terra

Già gli antichi Greci sapevano che, navigando verso Sud o verso Nord nel Meditteraneo, il cielo visibile cambia, le stelle assumono altezze e direzioni diverse e stelle mai visibili da un luogo diventano visibili da un altro. Da tutto ciò essi avevano correttamente dedotto la curvatura del nostro pianeta, almeno in senso Nord-Sud. Immaginiamo una bella notte invernale; telefoniamo ad un nostro amico che si trovi sul nostro stesso meridiano (quindi con la nostra stessa longitudine ), ma ad una latitudine più bassa, per esempio sulle coste della Libia. Immaginiamo di chiedergli di descriverci il cielo che vede sia verso Sud, sia verso Nord e confrontiamolo con ciò che vediamo noi. (Se avete qualche difficoltà usate le istruzioni per comprendere e leggere le seguenti cartine del cielo).

Il nostro amico vede, a Sud, per lo più le stesse stelle che vediamo noi, ma più alte; per esempio le tre stelle allineate della cintura di Orione (ORI) sono a poco più di 40° a Firenze e salgono a 60° in Libia. Vede però anche una stella che noi non vediamo mai: la brillante Canopo, tra la costellazione della Poppa (PUP) e quella del Pittore (PIC).

Verso Nord spicca la diversa altezza delle costellazioni circumpolari e della stella polare che appartiene all'Orsa Minore (UMI) e si trova sulla verticale del punto Nord dell'orizzonte. Gli antichi Greci si resero conto che il cielo è diverso anche se osservato in luoghi a diversa longitudine e dedussero così la curvatura della Terra anche in senso Est-Ovest. Per far ciò usarono le eclissi di Luna che permettono di sincronizzare l'osservazione fatta in luoghi lontani. Noi immaginiamo di telefonare ad un nostro amico che si trova, per esempio a Bucarest (quasi la stessa latitudine di Firenze, ma diversa longitudine) e di chiedergli di descriverci il cielo che vede, in modo da paragonare la sua descrizione con ciò che, nello stesso momento, stiamo vedendo.

Concentriamoci sulla costellazione dello Scorpione (SCO): a Firenze essa si trova immediatamente ad Est del meridiano.

Il nostro amico la vede invece spostata ad Ovest, mentre sta transitando sul meridiano. Notate che a Bucarest il tempo civile è avanti di un'ora rispetto a Firenze.

[Per tornare alla pagina precedente usare il bottone back del browser]

Marzo

Marzo: in questo mese si collocano i primi lavori agricoli dell'anno, dopo la pausa dell'inverno. Notate la data di passaggio tra il segno dei Pesci e quello dell'Ariete che segnava l'inizio della Primavera.

[Per tornare alla pagina precedente usare il bottone back del browser]

Maggio

Maggio: si celebra la bella stagione con una processione di ragazzi e ragazze che indossano abiti bordati di verde, "livrée de mai", la livrea di maggio. Un'usanza diffusa in tutta Europa.

[Per tornare alla pagina precedente usare il bottone back del browser]

Meridiani

La Terra ha una forma molto vicina alla sfera. In una sfera non ci sono punti particolari come sono i vertici, per esempio, di un cubo, ma se la sfera si mette a ruotare ecco che due punti della sfera assumono una grande importanza sono i poli dell'asse di rotazione. Sono cioè quei due punti, diametralmente opposti, in cui l'asse di rotazione incontra la superficie della sfera. Se consideriamo i piani che passano per l'asse di rotazione, vediamo che ognuno di essi taglia la sfera in spicchi. Si sbucci un'arancia per rendersene conto. Un qualsiasi cerchio ottenuto tagliando la sfera con un piano passante per l'asse di rotazione prende il nome di circolo meridiano o meridiano. Diversamente dai paralleli, i circoli meridiani sono tutti Grandi circoli ed uguali al Circolo equatoriale. Sulla Terra questo non è esattemente vero in quanto il nostro pianeta è leggermente schiacciato ed il diametro equatoriale è più lungo di circa 70 chilometri di quello polare.

[Per tornare alla pagina precedente usare il bottone back del browser]

Il Notturnale

Con il nome di Notturnale o Notturlabio o orologio notturno viene indicato uno strumento astronomico, usato per la misura del tempo mediante l'osservazione della stella polare e della posizione, rispetto ad essa, di due brillanti stelle dell'Orsa Maggiore. La costruzione di strumenti di questo tipo risale al XIII secolo.

Il Notturnale di Della Volpaia conservato presso l'Istituto e Museo di Storia della Scienza di Firenze L'orologio notturno ed in particolare quello rappresentato in figura è costituito tre dischi di ottone che possono ruotare l'uno rispetto all'altro attorno ad un anello centrale. Sporgente da questi tre dischi è un'asta o alidada, sporgente dal bordo del disco più grande, anch'essa libera di ruotare intorno all'anello ed indicante con lo spigolo rettilineo, tutte le possibili rette uscenti dal comune centro di rotazione.

Espoloso del Notturnale di Della Volpaia Lo strumento veniva puntato verso la stella polare che doveva essere traguardata attraverso il foro centrale, dopo aver impostato la data del giorno di osservazione. Il regolo mobile veniva ruotato fino a sovrapporsi con la congiungente le due stelle del Grande Carro, Dhube e Merak. Su i due dischi più interni venivano quindi lette le ore trascorse dalla mezzanotte e quelle trascorse dal tramnoto del giorno precedente. Questo tipo di strumenti, in mano ad un osservatore esperto poteva raggiungere l'accuratezza di 10 minuti.

Per meglio comprendere il funzionamento e l'uso dello strumento vi proponiamo di costruirvene uno, nell'ambito di un'esperienza didattica.

[Per tornare alla pagina precedente usare il bottone back del browser]

L'orologio notturno per la longitudine di Firenze (può funzionare in qualunque luogo)

A causa dei movimenti di rotazione e rivoluzione della Terra, l'aspetto del cielo notturno è diverso ad ore diverse dello stesso giorno ed alla stessa ora di giorni diversi. Le stelle vicine alla Polare, cioè alla direzione dell'asse terrestre, sono sempre visibili ad ogni ora di ogni notte dell'anno: dalla loro posizione possiamo facilmente dedurre l'ora o la data. In particolare le due stelle posteriori del "Grande Carro", Dubhe e Merak, risultano, almeno ad occhio nudo, allineate con la Polare e formano la lancetta delle ore di un grande orologio celeste. La lancetta compie un giro completo in 23 ore e 56 minuti, il tempo necessario alla Terra per ruotare di 360°, mentre il Sole, su cui regoliamo i nostri orologi, compie un giro completo in 24 ore.

La ragione di ciò è dovuta alla piccola distanza del Sole, relativamente alle stelle, per cui la Terra deve ruotare per circa 361° per riavere, il giorno dopo, il Sole nella stessa direzione, compensando così il suo spostamento orbitale. Il fenomeno è, in realtà, un po' più complicato perchè la Terra percorre intorno al Sole un'orbita ellittica a velocità variabile ed il suo asse è inclinato di circa 66° sul piano orbitale. Per questo motivo il tempo dell'orologio non è strettamente legato alla posizione del Sole Vero, il cui moto apparente è del tutto irregolare, ma alla Posizione del Sole Medio il cui moto è uniforme e che quindi ritorna, ogni giorno, nella stessa direzione dopo 24 ore esatte. Il nostro precedente ragionamento e la prima figura si riferiscono appunto al Sole Medio.

In figura è riportata la posizione della nostra lancetta alle ore 21 del quindicesimo giorno di ogni mese dell'anno: la posizione cambia di circa 30° al mese, poco meno di 1° al giorno. Se vogliamo utilizzarla per sapere che ore sono, dovremo disporre di un orologio con il quadrante delle ore mobile, in modo da poterlo ruotare in senso antiorario di circa un grado al giorno a partire da una posizione iniziale in cui, per esempio, le ore 21 del quadrante vengono indicate dalla nostra lancetta.

COSTRUZIONE ED USO L'orologio notturno che qui vi proponiamo, da ritagliare e montare, funziona proprio così. Lo strumento si compone di tre pezzi:

il disco dei mesi

il disco delle ore

il disco dell'alidada

Stampate su cartoncino colorato il primo ed il terzo e su plastica trasparente (su lucido) il secondo; ritagliateli lungo i loro bordi e montateli nell'ordine, uno sopra l'altro, congiungendoli con un rivetto forato di diametro non inferiore a 1 cm.

Lo strumento è ora pronto per l'uso. Si possono ottenere due risultati: l'ora della notte conoscendo la data oppure la data conoscendo l'ora.

Per realizzare le due misure è necessario individuare il Grande Carro e la stella Polare e rivolgere verso di essa lo strumento, in modo da traguardare la stella attraverso il foro del rivetto, tenendo l'orologio perpendicolare alla direzione che va dal vostro occhio alla stella ed avendo cura che la figura umana, stilizzata sul disco dei mesi, risulti correttamente orientata.

Determinazione dell'ora Dovete prima di tutto ruotare il disco delle ore fino a portare la freccia lunga, contrassegnata con FI, a coincidere con la data del giorno; poi, rivolto lo strumento verso la Polare, ruotate l'alidada fino a che il suo bordo diritto non sia allineato con la congiungente Dubhe-Merak. In corrispondenza della freccia dell'alidada si legge direttamente il tempo, sul disco delle ore. Determinazione della data Rivolgete lo strumento verso la Polare e ruotare l'alidada fino a che il suo bordo diritto non sia allineato con la congiungente Dubhe-Merak. Senza spostare l'alidada ruotare il disco delle ore fino a che il tempo corrente, segnato dal vostro orologio, sia indicato dalla freccia dell'alidada. La data è indicata dalla freccia lunga contrassegnata con FI del disco delle ore su quello dei mesi. Lo strumento può essere utilizzato in qualsiasi luogo dell'emisfero boreale nel quale il Carro sia sempre visibile su l'orizzonte, tuttavia la sua precisione è massima per i luoghi che si trovano a 3° o 4° ad Ovest del meridiano centrale del proprio fuso orario. Questa è appunto la situazione di Firenze. Possiamo adattarlo alla longitudine di altri luoghi semplicemente spostando la freccia sul disco delle ore. Avete tutti gli elementi per fare da voi questa operazione, tenendo anche conto che l'altra freccia sul disco delle ore è posizionata per i luoghi che si trovano lungo il meridiano centrale.

APPROFONDIMENTO Ho sviluppato la teoria su cui poggia l'orologio notturno in termini del tutto qualitativi, voglio ora mostrare la relazione quantitativa che lega insieme la posizione della lancetta, l'ora e la data. Le due stelle Dubhe e Merak sono effettivamente allineate con la Polare. La loro ascensione retta risulta rispettivamente:

Dubhe alpha UMA 11h:03m:44s Merak beta UMA 11h:01m:51s

Data la piccola differenza le possiamo considerare giacere sullo stesso meridiano celeste per cui, in ogni istante, il loro angolo orario è uguale e questa grandezza definisce la posizione della lancetta. La somma dell'angolo orario AO e della ascensione retta RA di qualsiasi oggetto celeste uguaglia il Tempo Siderale Locale TSL:

TSL = AO + RA Da questa relazione possiamo ricavare l'angolo orario delle due stelle conoscendo il Tempo Siderale Locale. TSL si ottiene dal Tempo Siderale di Greenwich (TSG) semplicemente aggiungendo, con il suo segno, la longitudine del luogo. Per convenzione la longitudine è positiva ad Est di Greenwich, negativa ad Ovest.

TSL = TSG + LONG TSG, infine, si ottiene a partire dal suo valore del primo giorno dell'anno alle ore 00:00 a Greenwich, TSG0h. Esprimendo TSG in ore abbiamo la seguente relazione:

TSG = TSG0h + 0.065709842 * d + 1.00273791 * TU dove

d è il numero progressivo indicante il giorno dell'anno, TU è il Tempo Civile a Greenwich, cioè il tempo trascorso dalla mezzanotte, la costante 1.00273791 è il rapporto tra il numero di ore siderali ed il numero di ore solari medie contenute in un eguale intervallo di tempo e permette quindi la trasformazione del tempo solare in tempo siderale, la costante 0.065709842 esprime in ore siderali la differenza tra un giorno siderale ed un giorno solare medio che è di circa 4 minuti: 0.065709842 ore = 3m 56.556s Possiamo esprimere TU in funzione del Tempo Civile TC di un Fuso Orario n (per convenzione n ha lo stesso segno della longitudine):

TU=TC-n Ed infine otteniamo:

TSL=TSG0h + k1 * d + k2 * (TC-n) + LONG Siamo ora in grado di esprimere la posizione della lancetta in funzione della data d e del tempo civile TC:

AODubhe=TSG0h + k1 * d + k2 * (TC-n) + LONG - ARDubhe Su questa formula si basa l'orologio notturno ed in particolare le sue scale lineari; vi è infatti una relazione di proporzionalità diretta tra la posizione della lancetta, la data ed il tempo civile. Sviluppando il prodotto nel secondo termine abbiamo:

AODubhe = TSG0h + k1 * d + k2 * TC-K2 * n+ LONG - ARDubhe la quantità K2 * n + LONG è la differenza in longitudine tra il luogo ed il meridiano centrale del corrispondente fuso orario. Resta quindi dimostrato che la posizione della lancetta è la stessa in tutti i luoghi aventi la stessa distanza in longitudine dal meridiano centrale.

TSG0h non è costante da un anno all'altro:

1990 TSG0h = 6.626 1991 TSG0h= 6.610 1992 TSG0h = 6.594 1993 TSG0h = 6.644 1994 TSG0h = 6.628 solo gli anni in fase con l'anno bisestile hanno all'incirca lo stesso valore, lo strumento è costruito per il secondo anno successivo a quello bisestile (il 1994, il 1998 per esempio) per cui negli altri anni si commette un errore massimo di due minuti. Questo errore è del tutto trascurabile perchè inferiore alla risoluzione di lettura delle scale ed alla inaccuratezza derivante dalla non concentricità dei dischi. Anche per anni in fase con quello bisestile TSG0h non riassume esattamente lo stesso valore; ciò è dovuto al fatto che l'anno del nostro attuale calendario è leggermente più lungo dell' anno tropico il che produce lo sfasamento di un giorno, tra calendario e stagioni in circa 4000 anni {la durata dell'anno tropico è di 365.2422 giorni solari medi e quella dell'anno del calendario 365.2425}. L'errore che ne deriva fa sentire i suoi effetti sullo zero delle scale in qualche migliaio di anni, quando questo orologio notturno non sarà più utilizzabile poichè la polare non sarà più nella direzione dell'asse terrestre a causa della precessione.

---

• Questo scritto è stato tratto dal manuale che accompagna il Notturlabio del Comitato per la divulgazione dell'Astronomia, realizzato da Piero Ranfagni.

[Per tornare alla pagina precedente usare il bottone back del browser]

Novembre

Novembre: il bosco fornisce l'ultima raccolta dell'anno, le ghiande preziose per l'ingrasso del maiale.

[Per tornare alla pagina precedente usare il bottone back del browser]

Scale non rotazionali

Una volta constatata la non uniformità di qualunque scala basata sulla rotazione terreste, nel 1956 l'Unione Astronomica Internazionale propose una nuova scala temporale che prese il nome di Tempo delle effemeridi (TE). L'intervallo di scala, il secondo delle effemeridi fu fissato, una volta per tutte, nella 31.556.925,9747-esima parte del tempo che fu necessario al Sole per passare dalla posizione che occupava alle ore 12:00 del 31 Dicembre 1899 alla stessa posizione l'anno dopo (anno tropico 1900). Questo significa che, dalla durata dell'anno 1900, si determinarono le costanti che intervengono nel calcolo del moto dei pianeti, inclusa la Terra e la Luna, e si ricava poi il tempo trascorso dal 1 Gennaio 1900, confrontando le posizioni assunte da questi astri, con quelle previste dalla teoria. Il tempo delle effemeridi, così definito, è una scala uniforme per definizione, in quanto è la variabile indipendente delle equazioni di moto dei pianeti e della luna. In linea di principio quindi, una determinazione del tempo delle effemeridi comporta un'osservazione delle posizioni del Sole e dela Luna. Le posizioni trovate andranno poi confrontate con quelle contenute in una tabella (effemeride), già calcolata, in cui le posizioni sono riportate in funzione del tempo (uniforme) delle effemeridi. Il valore di tempo per cui le posizioni calcolate e quelle osservate conicidono, è il tempo delle effemeridi cercato. Le misure che si debbono fare per determinare le posizioni della Luna e dei pianeti non sono molto precise ed, inoltre, il tempo lo si ottiene solo dopo complesse riduzioni dei dati raccolti. Il risultato finale di questo procedimento, che non è così banale come lo abbiamo descritto, dipende, in maniera sostanziale, dalle equazioni di moto e dalle tecniche di calcolo adotate per ottenere le effemeridi dei diversi corpi del sistema solare. Equazioni e metodi divengono molto complessi quando si cerca di tener conto delle reciproche perturbazioni gravitazionali. Per tutti questi motivi il tempo delle effemeridi non viene più usato come unità di misura, nemmeno per compilare le effemeridi astronomiche, nelle quali, dal 1984, è stato adottato il tempo dinamico terrestre che è un tempo atomico. Data la natura estremamente teorica ed elusiva del tempo delle effemeridi, viene da chiedersi che cosa aveva concretamente in mano l'utente finale, il geodeta ed il navigante, nel breve periodo (1956-1967) in cui questa scala è rimasta in vigore. L'utente disponeva sostanzialmente di un piccolo numero: la differenza tra tempo delle effemeridi e tempo universale in secondi, caratteristica per un determinato anno.

In questo modo disponeva delle posizione dei pianeti, del Sole e della Luna precise, perchè basate su una scala di tempo sicuramente uniforme, e di un valore per calcolare gli angoli orari degli astri, che dipendono dall'effettiva rotazione (non uniforme) della Terra.

Altre informazioni su questi argomenti in rete nei seguenti siti:

Time Service Department U.S. Naval Observatory, Washington, DC NEOSThe National Earth Orientation Service (NEOS)

[Per tornare alla pagina precedente usare il bottone back del browser]

Ottobre

Ottobre: si ara e si semina nei campi.

[Per tornare alla pagina precedente usare il bottone back del browser]

Ogigia

È l'isola del Mediterraneo occidentale in cui, secondo Omero, viveva Calipso. Molto probabilmente si tratta di un luogo immaginario in quanto ogni tentativo di identificazione è risultato inconsistente.

[Per tornare alla pagina precedente usare il bottone back del browser]

Paralleli

La Terra ha una forma molto vicina alla sfera. In una sfera non ci sono punti particolari come sono i vertici per esempio di un cubo, ma se la sfera si mette a ruotare ecco che due punti della sfera assumono una grande importanza sono i poli dell'asse di rotazione. Sono cioè quei due punti, diametralmente opposti, in cui l'asse di rotazione incontra la superficie della sfera. Se consideriamo i piani perpendicolari all'asse di rotazione che intersecano la sfera, vediamo che ognuno di essi taglia la sfera lungo cerchi il cui diametro è tanto più piccolo quanto più il piano è vicino ad un polo della sfera Questi cerchi vengono detti circoli paralleli o paralleli. Il cerchio più grande è detto cerchio equatoriale ed è quello che si ottiene tagliando la sfera con un piano equidistante dai due poli e quindi passante per il suo centro. I paralleli sono tutti Piccoli circoli con esclusione dell'Equatore che è un Grande circolo

[Per tornare alla pagina precedente usare il bottone back del browser]

Pitea, esploratore avventuroso (e fantasioso) del IV secolo a.C.

Pitea, navigatore greco originario della colonia di Massalia (la moderna Marsiglia), fu il primo greco a descrivere la costa nord-occidentale dell'Europa, compresa la Gran Bretagna. Il suo libro principale sull'"Oceano" è stato perduto, tuttavia le sue descrizioni sono state ampiamente copiate dai geografi che sono vissuti dopo di lui, in particolare Eratostene e Posidonio, altri invece come Polibio e Strabone considerarono le sue descrizioni come pure fantasie. Tuttavia, è sicuro che Pitea abbia veramente percorso le coste europee spingendosi molto a Nord; questa certezza deriva dalle descrizioni delle usanze dei popoli incontrati, ma soprattutto dalle indicazioni che Pitea dà sulla lunghezza dell'ombra dello gnomone al solstizio d'Estate a quelle latitudini. Tra le descrizioni di questo avventuroso navigatore greco troviamo anche quelle della lontana Tule, una città che si sarebbe dovuta trovare a sei giorni di navigazione delle coste settentrionali dell'Inghilterra, ed il cui territorio si estendeva verso il circolo polare artico.

[Per tornare alla pagina precedente usare il bottone back del browser]

Pleiadi

L'ammasso delle Pleiadi osservato con un binocolo astronomico Le Pleiadi costituiscono l'ammasso di stelle forse più famoso. Si trovano nella costellazione del Toro a Nord Ovest della stella più luminosa, Aldebran. Ad occhio nudo se ne vedono sette, difatti le Pleiadi sono note anche come le "sette sorelle". Con un buon binocolo, e con il cielo sufficientemente scuro, si scopre che l'ammasso, il cui diametro è all'incirca uguale a quello della Luna, è costituito da centinaia di stelle a cui è associata una debole nebulosità.

La costellazione del Toro da Johann Hevelius: URANOGRAPHIA (1690) (la freccia indica l'ammasso delle Pleiadi). L'immagine appartiene alla collezione storica del Museo astronomico di Brera, disponibile in rete . Nella cartografia celeste dell'epoca i punti cardinali Est ed Ovest risultano invertiti in quanto il cielo viene rappresentato come un globo celeste visto dall'esterno. Queste stelle hanno eccitato la curiosità fino dall'antichità e qualche volta sono state considerate esse stesse una costellazione. Per i Greci esse erano le figlie di Atlante e Pleione, che sono l'ottava e la nona stella del gruppo in ordine di luminosità decrescente. Secondo un'altra leggenda esse erano le compagne di caccia della dea Artemide, che, quando vennero molestate dal brutale cacciatore Orione, furono strappate alla terra dalla loro protettrice e poste in cielo. Spesso nelle leggenda vengono anche indicate come le stelle piangenti. Potrebbero piangere per la scomparsa di una sorella, la stella Sterope, che nel tempo si è molto indebolita e quindi si perde facilmente nell'osservazione ad occhio nudo.

[Per tornare alla pagina precedente usare il bottone back del browser]

La Precessione degli Equinozi

L'attrazione gravitazionale della Luna e del Sole tende a modificare la direzione dell'asse di rotazione terrestre facendole descrivere, in senso orario, la superficie di un cono in poco più di 26.000 anni. L'asse di questo cono è perpendicolare al piano dell'orbita terreste ossia dell'eclittica. Di conseguenza i poli celesti descrivono un cerchio attorno ai corrispondenti poli dell'eclittica, mantenendosi a 23° e 26' da essi. Il piano equatoriale è solidale con l'asse di rotazione, per cui i suoi punti d'intersezione con l'eclittica (chiamati il punto Gamma ed il punto Omega) scorrono lentamente in senso orario, muovendosi di circa 50" all'anno. Gli equinozi (il punto Gamma ed Omega) sembrano precedere le stelle verso il tramonto, da qui il nome di Precessione degli Equinozi che viene dato a questo fenomeno. Il punto Gamma, muovendosi apparentemente in senso orario lungo l'eclittica, va incontro al Sole che si muove, in senso antiorario, sullo stesso piano. Per questo motivo, l'anno tropico è di circa 20 minuti più breve dell'anno sidereo. L'anno tropico dura 365.2422 giorni, ovvero 365g 5h 49m, mentre l'anno sidereo 365.253 ovvero 365g 6h 9m. Il fenomeno della Precessione, modificando la posizione dell'Equinozio di Primavera rispetto alle stelle, comporta il cambiamento sia dell'ascensione retta che della declinazione. La Precessione degli Equinozi non ha praticamente alcun effetto sul pianeta Terra, in quanto lascia invariata l'inclinazione dell'eclittica, da cui dipende l'ampiezza della variazione stagionale dell'inclinazione dei raggi solari, che scaldano il suolo terrestre. La manifestazione più evidente della Precessione è lo spostamento del Polo Nord Celeste tra le stelle e quindi l'avvicendamento, nel tempo, delle stelle polari, cioè delle stelle luminose che, di volta in volta, risultano più vicine ad esso. Nelle cartine seguenti la lettera P indica il polo nord celeste.

Il cielo a Firenze a meta' di Aprile del 1998 La Polare attuale è la stella alfa Ursae Minoris (UMI), ma 2500 anni fa era Kosciab, la beta della stessa costellazione.

Il cielo a Firenze a metà di Aprile di 2500 anni fa e sarà la stella Vega, l'alfa della Lira (LYR) tra 11.000 anni

Il cielo a Firenze a metà di Aprile tra 11.000 anni Dalla variazione delle coordinate equatoriali delle stelle al passare del tempo, deriva anche che le stelle circumpolari (quelle che non sorgono nè tramontano in un dato luogo) possono diventare occidue (quelle che sorgono e tramontano) e le stelle occidue diventare invisibili (quelle che non sorgono mai) e viceversa.

Altre informazioni sulla precessione in rete nei seguenti siti:

Dimostrazione della Precessione nel laboratorio di Fisica Precession of the Equinoxes Una spiegazione completa, ma con tanta matematica Il mito di Mitra spiegato con la precessione.

[Per tornare alla pagina precedente usare il bottone back del browser]

Le proiezioni prospettiche

Le proiezioni prospettiche si distinguono in proiezioni polari, equatoriali o qualsiasi, a seconda che il polo di proiezione (punto di tangenza della sfera con il piano di proiezione) sia uno dei poli terrestri o si trovi sull'equatore o coincida con un punto qualsiasi della superficie terrestre. In ciascuno dei casi la proiezione potrà essere centrografica, stereografica, od ortografica, a seconda della posizione del punto vista. Nella proiezione centrografica, il punto di vista è al centro della sfera, in quella stereografica è nel punto diametralmente opposto al polo di proiezione, mentre in quella ortografica si trova all'infinito.

Nella pratica cartografica si rivelano molto più utili le proiezioni azimutali modificate, in modo da conservare, con opportuni algoritmi, alcune o tutte le proprietà cartografiche. Alcuni esempi:

La proiezione azimutale equidistante raffigurata è una proiezione polare, centrografica modificata. I meridiani sono rettilinei, i paralleli concentrici e volutamente ed arbitrariamente equidistanziati. In questo modo l'equidistanza è assicurata lungo ogni direzione a partire dal centro che, in questo caso, coincide con il polo geografico, essendo l'asse terrestre perpendicolare al piano di proiezione. Le lossodromiche che si irradiano dal centro coincidono con i meridiani e sono quindi rettilinee.

Anche in questo caso la proiezione e' polare, centrografica e modificata. La modifica consiste nel garantire l'equivalenza delle superfici. In questa proiezione i paralleli non sono equidistanziati e tendono ad avvicinarsi verso la periferia della carta.

La proiezione stereografica è una proiezione puramente geometrica, non modificata. Quella raffigurata è polare con il punto di vista nel Polo Sud geografico. Nella proiezione stereografica gli angoli compresi tra due circoli sulla sfera vengono conservati sulla carta. quindi la proiezione è isogonica e conforme: i continenti mantengono la loro forma. Questo non è però vero per le aree, che aumentano dal centro alla periferia.

La proiezione gnomonica raffigurata è equatoriale e centrografica, puramente geometrica. Non è conforme, nè equidistante, ma le distorsioni sono piccole al centro e crescono alla periferia, dove diventano intollerabili. Ha una proprietà unica: ogni grande circolo risulta essere rettilineo, qualunque sia la sua direzione. Conseguentemente l'equatore e tutti i meridiani sono rettilinei, ma non lo sono i paralleli.

La proiezione ortografica qui rappresentata è una proiezione obliqua, poichè il piano è tangente alla sfera terrestre non lungo l'equatore, ma lungo un parallelo. In questo tipo di proiezione si hanno poche e trascurabili distorsioni attorno al centro, ma evidenti compressioni quando ci si allontana da esso.

[Per tornare alla pagina precedente usare il bottone back del browser]

Rallentamento della velocità di rotazione della Terra

Negli anni '30 fu dimostrato che le posizioni apparenti del Sole, della Luna e dei pianeti, calcolate per un'epoca abbastanza lontana, usando come unità di tempo il secondo definito come la 86.400-esima parte del giorno attuale, risultavano sistematicamente spostate ad Ovest, rispetto alle loro posizioni documentate storicamente, in occasione di qualche evento eccezionale come le eclissi di Sole o di Luna. Questo significava che la velocità di rotazione della Terra era, nel passato, maggiore di adesso e che il nostro pianeta stava progressivamente rallentando. Sappiamo che il fenomeno è dovuto principalmente alla dissipazione dell'energia meccanica di rotazione della Terra, attraverso gli attriti che si generano per gli scorrimenti di grande masse liquide e le deformazioni di grandi masse solide, causate dalle maree. Ma le cose non sono semplici, perchè assistiamo ad una variazione del rallentamento in parte periodica, legata alle variazioni stagionali, ed in parte del tutto irregolare e non compresa. Se ci limitiamo alla componente costante della decelerazione angolare della Terra, sulla base delle osservazioni astronomiche di 2000 anni, si ottiene il valore:

Un fenomeno governato da un numero così piccolo parrebbe del tutto trascurabile, invece i picccoli ritardi si accumolano e producono differenze, tra le posizioni calcolate e le posizioni osservate, misurabili già dopo pochi anni. Partiamo da un situazione iniziale al tempo in cui la Terra ha velocità angolare , pari a 360° al giorno. Dopo giorni, misurati da un orologio perfetto, che batta il secondo uguale alla 86.400-esima parte del giorno iniziale, avremo una velocità

e la Terra avrà ruotato di un angolo che non contiene un numero intero di angoli giri, cioè di rotazioni complete.

Dopo 36.525 giorni, cioè un secolo, il giorno si è allungato di soli 2 millesimi di secondo, ma la differenza tra l'angolo orario di una qualunque stella, osservato e previsto, sulla base dell'orologio sincronizzato con il giorno di partenza, è già di 36 secondi, più di 548 secondi d'arco. Dopo duemila anni la differenza è di oltre 4 ore, più: di 60° !

1 secolo 2 secoli 4 secoli 6 secoli 8 secoli 10 secoli 15 secoli 20 secoli 36 secondi 2.5 minuti 9.7 minuti 21.9 minuti 38.9 minuti 1.01 ore 2.28 ore 4.06 ore

Altre informazioni su questi argomenti in rete nei seguenti siti:

Time Service Department U.S. Naval Observatory, Washington, DC Il Tempo di Internet (in italiano)

[Per tornare alla pagina precedente usare il bottone back del browser]

Scale rotazionali

Il fenomeno più evidente, causato dalla rotazione e dalla rivoluzione della Terra, è l'alternarsi del giorno e della notte. Si tratta di due intervalli di tempo variabili da un giorno all'altro e dipendenti dalla latitudine dell'osservatore, come risulta dalla tabella, in cui l'ora del sorgere e del tramontare del Sole è espressa in tempo civile (TC), segnato dai comuni orologi.

LUOGO DATA ALBA TRAMONTO DURATA Firenze 1 Ottobre 1998 06:13:46 17:55:13 11h 35m 9s (43° 45' N) 30 Ottobre 1998 06:49:32 17:07:30 10h 11m 8s Napoli 1 Ottobre 1998 06:00:50 17:44:24 11h 37m 33s (40° 52' N) 30 Ottobre 1998 06:32:29 17:00:47 10h 21m 48s

I Greci ed i Romani dividevano in 12 parti uguali l'arco diurno percorso dal Sole, ottenendo così ore di diversa durata a seconda del giorno dell'anno, le ore temporarie. Alla latitudine di Roma l'ora invernale diurna durava circa 45 minuti e l'ora estiva circa 75 (con riferimento, ovviamente, ai nostri attuali minuti). Gli apparecchi usati per misurarle erano il Polos e lo Gnomone. Il Polos è una specie di tazza semisferica sulla quale si proietta l'ombra di uno stilo orizzontale. Durante il giorno il vertice dell'ombra traccia un cammino arcuato che è la proiezione dell'arco diurno percorso dal Sole in cielo. Lo strumento porta incisi i percorsi diurni dell'ombra per alcuni giorni dell'anno, solitamente gli equinozi ed i solstizi. Questi archi sono divisi in parti ugauli da altri archi appartenenti a circoli meridiani convergenti nel piede dello stilo: le linee orarie.

Il Polos della figura è conservato a Roma, in Vaticano. Si riconoscono 11 linee orarie e 7 percorsi diurni, corrispondenti a ciascun mese dell'anno. I mesi simmetrici, rispetto ai solstizi, sono rapprentati dallo stesso percorso, in quanto il Sole assume gli stessi valori di declinazione: Maggio e Luglio, Novembre e Gennaio ecc.

Con lo Gnomone l'ora temporaria può essere ricavata misurando la lunghezza dell'ombra proiettata. La lunghezza è diversa non solo ad ore diverse dello stesso giorno, ma anche alla stessa ora di giorni diversi, per cui era necessario corredare lo strumento con tabelle di lunghezze, come quelle che troviamo nell' "Opus Agriculturae" dell'agronomo romano Palladio.

HORA LUNGHEZZA I et XI Pedes XXIX II et X Pedes XIX III et IX Pedes XV IV et VIII Pedes XII V et VII Pedes X VI Pedes IX

L'ora VI coincideva con l'ombra più corta della giornata e corrispondeva alla culminazione del Sole, il nostro mezzogiorno. Entrambi questi strumenti cessavano di funzionare, se trasportati in luoghi a latitudine diversa da quella per la quale erano stati costruiti o calcolati. I Romani, per molto tempo, non ne capirono la teoria e continuarono a lamentarsi che i Polos, accumolati nel foro e provenienti da luoghi diversi, a seguito delle campagne militari, non andavano d'accordo!!

Una scala più uniforme venne ottenuta dividendo in 24 parti uguali il tempo che intercorre tra due culminazioni successive del Sole, il giorno solare vero. Le ore così definite sono quasi uguali in tutti i giorni dell'anno ed hanno circa la stessa durata delle nostre. Vennero chiamate ore equinoziali perchè coincidono con le temporarie agli equinozi, quando l'arco diurno del Sole è uguale a quello notturno. Gli strumenti che le misurano sono, da una parte gli astrolabi e le armille utilizzate solo dagli astronomi, e dall'altra le meridiane, veri e propri orologi pubblici che, dalla fine del XV secolo, sono presenti in tutta Europa. Il termine meridiana è errato, sarebbe meglio chiamarli orologi solari perchè solo alcuni di essi sono meridane, cioè quelli che indicano quando il Sole si trova in meridiano. Tuttavia in Italia ed in Toscana in particolare, si usa il termine meridiana per indicare un qualsiasi orologio solare.

Il principio di funzionamento della meridiana era sicuramente noto anche ai tempi di Tolomeo, ma non fu utilizzato, fuori dall'ambito strettamente astronomico, perchè in quelle società le ore uguali non erano richieste. Le ore uguali vengono introdotte negli usi civili dalle società mercantili del basso medioevo, quando il tempo di produzione delle merci viene incorporato, come valore aggiunto, nel loro costo. Nell'orologio solare la lancetta è data dall'ombra di uno stilo parallelo all'asse della Terra. La direzione dell'ombra di uno stilo parallelo all'asse della Terra, raccolta su una superfice qualsiasi, è sempre la stessa per uguali valori dell'angolo orario del Sole, in qualunque giorno dell'anno. Ma anche le ore equinoziali non costituiscono una scala uniforme, in quanto il giorno solare vero non è costante, a causa dell' eccentricità dell'orbita terrestre e dell'inclinazione dell'asse di rotazione sul piano orbitale. Consideriamo a mò di esempio i tempi di culminazione (il mezzogiorno solare vero locale) a Firenze in due giorni del Dicembre 1998.

DATA MEZZOGIORNO VERO TEMPO INTERCORRENTE 1 Dicembre 1998 12:03:59 2 Dicembre 1998 12:04:22 24h 0m 23s 29 Dicembre 1998 12:16:59 30 Dicembre 1998 12:17:28 24h 0m 29

In un giorno vi sono 24 ore, in un'ora 60 minuti ed in un minuto 60 secondi. Quindi in un giorno 60X60X24 = 86.400 secondi. Se definiamo il secondo come la 86.400-esima parte del giorno solare vero, l'unità definita il 1 Dicembre risulterà più corta di quella definita alla fine del mese. La diversa durata del giorno solare vero era già nota agli astronomi greci che la deducevano dalla diversa durata delle stagioni.

STAGIONE DURATA Primavera 92g 20.2h Estate 93g 14.4h Autunno 89g 18.7h Inverno 89g 0.5h

Con la rivoluzione industriale esigenze civili e tecnico-scientifiche impongono che il secondo sia rigorosamente costante. Nel 1700 viene introdotto, anche nella vita civile, un artificio astronomico-matematico: il Sole medio. Si tratta di un corpo fittizio che percorre l'equatore celeste con velocità angolare costante, nello stesso tempo in cui il Sole vero percorre l'eclittica. L'angolo orario del sole medio, contato a partire dall'antimeridiano locale, prende il nome di Tempo Solare Medio. Tra tempo solare vero e tempo solare medio vi è una differenza che varia di giorno in giorno, con il sole vero che talvolta segue e talvolta precede il sole medio. Questa differenza prende il nome di Equazione del tempo e può essere calcolata dagli elementi orbitali della Terra, per ogni giorno dell'anno.

Il tempo solare medio è un tempo locale e quindi dipende dalla longitudine dell'osservatore; sono sufficienti pochi chilometri per avere differenze apprezzabili. La tabella dà il tempo solare vero locale (TSVL) e quello medio locale (TSML) per Firenze ed Arezzo, nello stesso istante del 26 Novembre 1998, quando gli orologi segnavano le ore 12:00.

LUOGO TSVL TSML Arezzo 11:59:38 11:47:00 Firenze 11:57:39 11:45:01

Per ovviare a ciò la Terra è stata divisa in 24 spicchi meridiani chiamati Fusi Orari. Si è definito Tempo Civile di ogni luogo all'interno del fuso, il tempo solare medio, misurato lungo il meridiano centrale del fuso. La differenza tra i tempi locali di due luoghi è pari alla differenza delle loro longitudini, espresse in ore, minuti e secondi di tempo. La tabella indica la differenza di 21 secondi tra i tempi locali di Firenze ed Arezzo. Questo valore deriva dalle loro longitudini; Firenze 11° 15' 19" Est, Arezzo 11° 45' Est.

Per la determinazione delle longitudini e per le osservazioni astronomiche si usa il Tempo Universale (TU), che è il tempo solare medio misurato a Greenwich. L'origine della scala è fissata alla culminazione inferiore (mezzanotte) a Greenwich del sole medio, e l'unità di scala, il secondo, è definita come la 86.400-esima parte del giorno solare medio.

A dispetto delle definizioni il tempo universale non viene misurato direttamente; non è facile misurare la posizione del Sole con grande precisione, dal momento che non è non è un oggetto puntiforme. Si preferisce determinare (usando particolari canocchiali chiamati strumenti dei passaggi) l'istante esatto della culminazione meridiana di alcune stelle di cui si conoscono, con grande esattezza, le coordinate equatoriali che vengono corrette per la precessione ed altri effetti minori. Alla culminazione l'angolo orario di un corpo celeste è nullo e la sua ascensione retta è uguale al tempo siderale locale. Da questo si ricava poi, con il calcolo, il tempo universale. Il tempo universale è strettamente legato al tempo siderale e fornisce la posizione della Terra rispetto alla stelle. La sua conoscenza è essenziale in Geofisica, Topografia, Navigazione marittima e spaziale. Contrariamente al Sole, le stelle sembrano trascinate dal moto regolare della sfera celeste, dovuto a quello di rotazione della Terra. Il tempo che intercorre tra due culminazioni successive di una qualsiasi stella prende il nome di Giorno siderale e, da un giorno all'altro, appare essere assolutamente costante. Per millenni il moto di rotazione apparente della sfera celeste, e per secoli quello reale della Terra, sono stati considerati assolutamente uniformi. Ma non è così: la Terra sta rallentando e la durata del giorno siderale aumenta di due millesimi di secondo ogni 100 anni. Eulero lo sospettò fin dalla fine del XVIII secolo per ragioni teoriche e nel 1936 lo si dimostrò, ricalcolando le date e gli orari di antiche eclissi e confrontando i risultati con le testimonianze storiche. Diverse sono le cause che rendono non uniforme la rotazione della Terra. L'attrito delle maree è il maggior responsabile: una parte dell'energia meccanica della rotazione viene dissipata sotto forma di calore. Spostamenti di grandi masse di acqua e di aria causano variazioni stagionali della sua velocità. A tutto questo si aggiunge poi una variabilità accidentale, talvolta positiva, talvolta negativa. Non esiste una soddisfacente descrizione quantitativa di tutte queste cause, per cui non è possibile correggere a priori le osservazioni, in modo da rendere uniforme la scala di tempo universale. Per questo motivo l'unità di scala, il secondo di tempo universale, non è più in vigore dal 1956, quando fu sostituito dall'unità di una scala non rotazionale: il secondo del Tempo delle Effemeridi.

Altre informazioni su questi argomenti in rete nei seguenti siti:

Orologi solari Breve storia Unione Astrofili Italiani - Sezione Quadranti Solari Information Leaflets Prontuario di astronomia (in inglese) The National Earth Orientation Service (NEOS) Il servizio U.S.A. che si occupa delle variazioni della rotazione terrestre (in inglese)

[Per tornare alla pagina precedente usare il bottone back del browser]