Cosmologia per tutti

Le misure astronomiche

 di Claudio Del Duca

Sommario

Un disordinato testo di storia cosmica
 La notazione esponenziale
Unità di misura in astronomia
Le stelle fisse
La misurazione delle distanze (Parallasse trigonometrica)
Luminosità e distanze

 

Un disordinato testo di storia cosmica 

Quando alziamo gli occhi al cielo per osservare un qualunque corpo celeste luminoso, effettuiamo un viaggio nel tempo senza rendercene conto. È come aprire un libro di storia che riporta disordinatamente le vicende accadute in un tempo relativo allo spazio che ci separa dalle stesse. Infatti, le onde elettromagnetiche della luce viaggiano nel vuoto alla velocità costante di 299.791 Km al secondo, ma, nonostante questa velocità elevatissima, per arrivare fino a noi impiegano sempre del tempo. È così che le radiazioni del Sole, dalla distanza media di 149,6 milioni di Km dalla Terra, ci arrivano mediamente dopo 8 minuti e 20 secondi. Persino quando guardiamo la Luna, bisogna considerare che non la vediamo come e dove realmente è nel momento dell’osservazione, ma come e dov’era 1,31 secondi prima. Lo stesso discorso vale per gli altri pianeti del Sistema Solare, per le altre stelle della Via Lattea e per le altre galassie che riusciamo ad osservare solo con adeguate strumentazioni ottiche e radio. La realtà contemporanea dell’Universo è dunque assai diversa dalla realtà percettiva che ne abbiamo perché possiamo osservare solo ciò che ha emesso o riflesso una qualche radiazione in un preciso momento del passato più o meno remoto in relazione alla distanza della fonte.

La notazione esponenziale

Gli astronomi hanno a che fare con numeri o molto grandi o molto piccoli e, quindi, per ragioni di praticità usano, per tali grandezze, la cosiddetta notazione esponenziale. Un numero come 3.000.000 viene dunque espresso come 3 x 106. In generale, un qualsiasi numero viene espresso nella forma X,XXX x 10n dove n è il numero di zeri che devono essere aggiunti al numero o il numero di posti di cui deve essere spostata la virgola decimale verso destra. Se l'esponente è negativo, la virgola deve essere spostata verso sinistra, ovvero 6 x 10-2 equivale a 0,06.

Ecco alcuni equivalenti: ;103 = mille, 106 = un milione, 109 = un miliardo.

 

Unità di misura in astronomia

Gli astronomi, a causa dell'immensità delle distanze che caratterizzano il loro campo di studio, si servono di varie unità di misura speciali. L’uso di queste unità rende le loro descrizioni più concise e facilita i calcoli più impegnativi. Ecco le unità di misura astronomiche più importanti: unità astronomica, anno-luce, parsec, kiloparsec, megaparsec.

Unità astronomica (UA): è la distanza media fra il Sole e la Terra, che è grosso modo di 149 600 000 km. Quest'unità viene usata per lo più per misurare le distanze all’interno del Sistema Solare o fra coppie di stelle molto vicine fra loro. Una UA equivale anche a 499 secondi-luce (8 minuti-luce e 19 secondi-luce), tempo impiegato dalla luce a percorrere la distanza Sole-Terra.

Anno-luce:  
la distanza che la luce, o qualsiasi altra radiazione elettromagnetica, percorre in un anno nel vuoto. Questa distanza è pari a circa 63 240 UA, (9 460,704 miliardi di chilometri) una distanza sufficiente per potervi allineare 800 sistemi solari l’uno accanto all’altro.

Parsec (Pc):  
gli astronomi usano quest’unità di misura per misurare distanze fuori del nostro sistema solare. Essa è usata talvolta invece dell’anno-luce per grandi distanze.
Parsec è un’abbreviazione per parallasse-secondo . Un parsec è la distanza alla quale una stella avrebbe una parallasse di 1" e corrisponde a 206.265 UA, a 3,086 x 1013 Km o a 3,262 anni-luce. (206.265 è il numero di secondi contenuti in un radiante). Il Sole, che dista da noi 1 UA, ha una parallasse di 206 265 secondi. 1° è uguale a 60’ e a 3600’’ (vedi Parallasse trigonometrica).

Kiloparsec  (Kpc):
usando gli usuali prefissi del sistema metrico, 1000 parsec diventano 1 kiloparsec. Spesso le distanze all’interno della Via Lattea vengono date in kiloparsec. Il kiloparsec è pari, ovviamente, a 3 260 anni-luce. Il nostro sole si trova a circa 8,5 kiloparsec dal centro della Via Lattea.

Megaparsec  (Mpc):
Le distanze di altre galassie vengono misurate di solito in megaparsec che è pari a un milione di parsec. Questi numeri vengono di solito arrotondati a causa delle grandi incertezze con cui conosciamo queste distanze immense.

Le stelle fisse

L’osservazione della volta celeste ha portato gli antichi ad immaginare che la Terra fosse immobile nello spazio. Si dedusse che le stelle fossero “fissate” su una grande sfera cristallina che nel corso del giorno compiva un giro completo attorno alla Terra. Per questo motivo esse furono chiamate “stelle fisse”. Solo fra la fine del 400 all’800, secoli in cui vissero Copernico, Galilei, Keplero e Newton, si comprese che le stelle non sono distribuite su una sfera, ma poste a distanze molto diverse.  L’apparente fissità delle stelle è dovuta al fatto che la loro distanza dalla Terra è così grande rispetto ai loro spostamenti che, chi osserva non può scorgere nessun cambiamento notevole nelle loro posizioni. Nel corso dei millenni, invece, il movimento delle stelle porta anche a mutare la forma delle costellazioni. Tra centomila anni, per esempio, l’Orsa Maggiore avrà una forma completamente diversa dall’attuale e assomiglierà grosso modo a una y. 
Per convenzione, oggi s’intendono “fisse” quelle stelle che sono abbastanza distanti da non mostrare alcun cambiamento di posizione con quelle apparentemente vicine nella volta in un periodo di sei mesi di osservazione (vedi sotto parallasse trigonometrica).

La misurazione delle distanze

La precisione in astronomia è estremamente relativa. Persino le distanze all’interno del nostro sistema solare vengono costantemente precisate man mano che veicoli interplanetari e satelliti artificiali inviano i loro dati alla Terra. In generale, con una certa esattezza si può dire solo che le distanze minori sono note con più precisione delle distanze maggiori. Ciò continuerà a essere vero anche al migliorare delle tecnologie per la misurazione delle distanze cosmiche.
Per determinare la posizione di una stella ci si serve della triangolazione partendo da due punti che definiscono una linea di base. Questo procedimento viene chiamato parallasse trigonometrica.

 Innanzitutto si misura la posizione della stella rispetto a quelli che consideriamo oggetti lontani di fondo, poi, sei mesi dopo, si prende un’altra misurazione della posizione apparente della stella quando la Terra si troverà, nel suo percorso orbitale, dalla parte diametralmente opposta rispetto al Sole. 

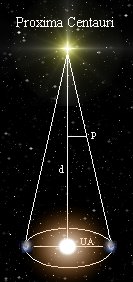Un oggetto, osservato da due punti opposti dell’orbita terrestre, a sei mesi di distanza, sembrerebbe mutare la sua posizione in cielo. La metà di questo angolo (p) è chiamata parallasse della stella. L’unità di misura di questi angoli è il secondo d’arco (1"). Le parallassi sono sempre minori di 1". La Proxima Centauri, la stella più vicina alla Terra, ha una parallasse di 0,765" e la 61 Cygni una parallasse di 0,293".

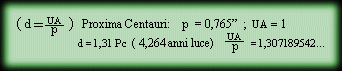
In questo modo si viene ad avere fra i due punti dell’orbita terrestre una linea di base di 299 milioni di Km. Gli astronomi prendono in realtà molte misurazioni fino a determinare la linea di base più lunga per un particolare oggetto. Persino disponendo di linee di base così lunghe possono verificarsi imprecisioni a causa dell’atmosfera terrestre e delle limitazioni nell’equipaggiamento. Questi margini di errore in astronomia scompaiono negli arrotondamenti. Il margine d’errore della parallasse trigonometrica per distanze fino a 10 anni-luce dalla Terra è inferiore al 3 %. Ci sono poche stelle note entro questa distanza, e alcune appartengono allo stesso sistema. 

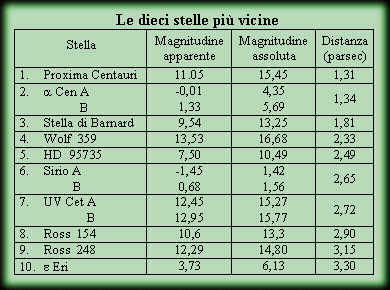
A distanze di 30 anni-luce si ritiene che il margine d’errore delle misurazioni sia del 10 %. Le distanze di stelle che si trovano a 100 anni-luce possono essere sbagliate del 30 %, e questa distanza è generalmente considerata il limite per misurazioni ragionevolmente esatte.

Se 100 anni-luce sono il limite usuale per tali tecniche trigonometriche, in che modo gli astronomi misurano la nostra Via Lattea, la quale ha un diametro stimato di 100.000 anni-luce? Raccogliendo la luce di stelle lontane su lastre fotografiche e studiandone gli spettri: una tecnica chiamata spettroscopia stellare. Stelle vicine la cui distanza è stata misurata con la parallasse possono essere usate come candele per lo studio di stelle simili che si trovano a distanze maggiori. Queste stelle ci appaiono poco luminose, ma solo perché sono molto lontane. Una volta che sia stato determinato il tipo spettrale di una stella lontana e che la si sia confrontata con stelle più vicine, è possibile determinarne la luminosità reale. Conoscendo la luminosità reale di una stella e la sua luminosità apparente dalla Terra, è possibile stimarne la distanza. Questo metodo indiretto di determinazione della distanza, che si può usare con elevata approssimazione anche per determinare la distanza di galassie lontane, è noto come parallasse spettroscopica. Studiando lo spettro della luce si è stimata la distanza di migliaia di stelle in tutta la nostra galassia (vedi Luminosità e distanze sottostante). Un altro metodo di misurazione delle distanze intergalattiche ci è fornito dal rilevamento dell’effetto doppler. Le righe spettrali scure presenti nella luce di un oggetto che si sta allontanando da noi sono spostate verso lunghezze d’onda maggiori, verso l’estremo rosso dello spettro. La luce rossa è quella che ha la lunghezza d’onda massima fra tutti i colori visibili. Si parla in proposito di sposmento verso il rosso. Se invece l’oggetto si sta avvicinando succede l’opposto: le lunghezze d’onda risultano compresse e si verifica uno spostamento verso il blu. Quanto maggiore è lo spostamento verso il rosso di un oggetto cosmico, tanto più lontano esso si trova nello spazio e nel tempo e tanto maggiore è la sua velocità di regressione nell’universo in espansione. Gli spostamenti verso il rosso dello spettro sono essenziali, assieme al valore della costante di Hubble, per determinare velocità e distanze di oggetti cosmici molto lontani.

Luminosità e distanze  

Le stelle più luminose sono designate con un nome proprio e le stelle di una stessa costellazione vengono indicate per ordine decrescente di luminosità mediante una lettera dell’alfabeto greco seguita dal genitivo latino della costellazione cui appartengono. Lo splendore con cui ci appare una stella in cielo dipende da due fattori: la luminosità e la distanza. La luminosità è la quantità di energia emessa dalla stella, sotto forma di radiazione, nell’unità di tempo e in tutte le direzioni, e dipende dalle dimensioni della stella e dalla temperatura superficiale. 
Tale quantità si può esprimere in funzione della luminosità solare che è nota (3,9 x 1033 erg/sec). Luminosità 10 significa perciò una stella che emette in un secondo energia radiativa 10 volte più del Sole. Nel II secolo a.C., Ipparco divise le stelle visibili a occhio nudo in sei gruppi. Le stelle più splendenti furono dette di “prima magnitudine” e le più deboli, al limite della percezione dell’occhio, di “sesta magnitudine”. 
Nel XIX secolo si scoprì che le stelle di prima magnitudine erano circa cento volte più luminose di quelle di sesta. Venne quindi adottato un nuovo sistema di magnitudini basato sulla definizione che ad una differenza di cinque magnitudini corrisponde esattamente un rapporto di intensità uguale a cento. Per poter includere nel nuovo sistema le stelle molto brillanti, la scala fu estesa ai numeri negativi. Sirio, la stella più splendente nel cielo, ha una magnitudine di -1,4. Analogamente, la scala fu ampliata alle stelle più deboli della sesta magnitudine, ossia alle stelle osservabili solo con telescopi. L’undicesima magnitudine corrisponde quindi a stelle cento volte più deboli della sesta e la sedicesima magnitudine corrisponde a stelle cento volte più deboli dell’undicesima. Le stelle più deboli, fotografabili con i più grandi telescopi, sono circa della venticinquesima magnitudine.
A seconda del particolare rivelatore usato (occhio, lastra fotografica, cellula fotoelettrica, ecc.), corrispondono differenti tipi di magnitudine. Va sottolineato che si parlerà di magnitudine apparente ogni volta che ci si riferisce alla luminosità di un oggetto qual è misurata dall’osservatore, senza tener conto dell’effetto della distanza sulla luminosità. Lo splendore apparente di una stella, quindi, dipende dalla distanza. Se il Sole, per esempio, si trovasse alla distanza di 100 anni-luce, non sarebbe visibile ad occhio nudo. Per eliminare l’effetto dovuto alle diverse distanze, si introduce la “magnitudine assoluta”, ossia la magnitudine che le stelle avrebbero se fossero tutte poste alla stessa distanza. Per convenzione, si fissa questa distanza a 10 parsec. Per determinare la luminosità di una stella è necessario conoscerne la distanza e la magnitudine. 

 

Indice Cosmologia